22)

Evaluation of the different terms in equation (

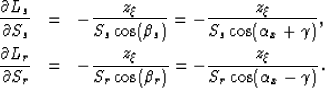
We show in Appendix A (equations (41) and (45))

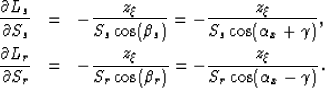$$\begin{eqnarray} \frac{\partial z_{\tilde{\gamma}}}{\partial L} = \frac{\cos ^2 ... ...\gamma} + \frac{\sin \gamma}{\cos \alpha_x} \tan \widehat{\gamma},\end{eqnarray}$$ (23)

and

$$\begin{eqnarray} \frac{\partial L_s}{\partial S_s} &=& - \frac{z_\xi}{S_s\cos(\... ...z_\xi}{S_r\cos(\beta_r)}=- \frac{z_\xi}{S_r\cos(\alpha_x-\gamma)}.\end{eqnarray}$$ (24) (25)

Using equations (23), (24) and (25), the relationship of the imaging depth in the angle domain with respect to perturbations in the anisotropic parameters can eventually be written as follows:

$$\begin{eqnarray} \frac{\partial z_{\tilde{\gamma}}}{\partial \rho_{i}} = -\frac{... ...(\alpha_x-\gamma)} \frac{\partial S_r}{\partial \rho_{i}} \right).\end{eqnarray}$$ (26)

This is the fundamental equation of this section, extending the equation given in Biondi (2005a) to include dipping reflectors.

The residual moveout $\Delta z_{\rm RMO}$ is defined as the difference between the reflector movement at finite aperture angle and the reflector movement at normal incidence. The latter is given by

$$\begin{eqnarray} \left.\frac{\partial z_{\tilde{\gamma}}}{\partial \rho_{i}}\rig... ...ight)} \frac{\partial S\left(\alpha_x \right)}{\partial \rho_{i}}.\end{eqnarray}$$ (27)