




Next: Example 1 - 2-D
Up: Acoustic wave-equation in 3D
Previous: One-way wavefield extrapolation
The extrapolation wavenumber defined in
equations 14 and 15 cannot be
implemented purely in the Fourier domain due to the presence of
mixed-domain fields (i.e. a function of both 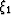 and
and 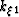 simultaneously). This can be addressed using an extended version of
the split-step Fourier approximation Stoffa et al. (1990), a
popular approach that uses Taylor expansions to separate
simultaneously). This can be addressed using an extended version of
the split-step Fourier approximation Stoffa et al. (1990), a
popular approach that uses Taylor expansions to separate 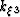 into
two parts:
into
two parts: 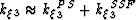 . Wavenumbers
. Wavenumbers 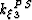 and
and 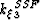 represent a pure Fourier domain phase-shift and a
mixed
represent a pure Fourier domain phase-shift and a
mixed 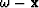 domain split-step correction, respectively.
domain split-step correction, respectively.
The phase-shift term is given by,
| ![\begin{displaymath}
k_\xi_3^{PS} =
- b_1 k_\xi_1
- b_2 k_\xi_2
+ i b_3
\pm
\le...
... i\,k_\xi_1
+ b_9 i\,k_\xi_2
- b_{10}^2
\right]^{\frac{1}{2}},\end{displaymath}](img37.gif) |
(16) |
where 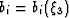 are reference values of
are reference values of 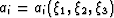 .
The split-step approximation is developed by performing a Taylor
expansion about each coefficient ai and evaluating the results
at stationary reference values bi. The stationary values of
.
The split-step approximation is developed by performing a Taylor
expansion about each coefficient ai and evaluating the results
at stationary reference values bi. The stationary values of
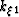 and
and 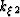 are assumed to be zero. This leads to a
split-step correction of,
are assumed to be zero. This leads to a
split-step correction of,
| 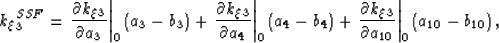 |
(17) |
where ``'' denotes "with respect to a reference medium". The
partial differential expressions in equation 17 are,
| 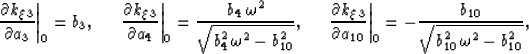 |
(18) |
resulting in the following split-step Fourier correction,
| 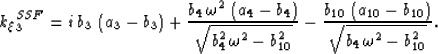 |
(19) |
Note that we could use many reference media followed by interpolation
similar to the phase-shift plus interpolation (PSPI) technique of
Gazdag and Sguazzero (1984).
Importantly, even though there are additional ai coefficients in
the dispersion relationship, these can be made smooth through mesh
regularization such that fewer sets of reference parameters are needed
to accurately represent wavenumber 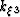 . In addition, situations
exist where some coefficients are zero or negligible. For example,
the coefficients for a weakly non-orthogonal coordinate system
(i.e.
. In addition, situations
exist where some coefficients are zero or negligible. For example,
the coefficients for a weakly non-orthogonal coordinate system
(i.e. 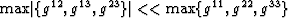 ) within a kinematic approximation reduce
to,
) within a kinematic approximation reduce
to,
| ![\begin{displaymath}
\mathbf{a}
\approx
\left[
0 \;\;\;
0 \;\;\;
0 \;\;\;
\ss / ...
... \;\;\;
0 \;\;\;
0 \;\;\;
n_3 / m^{33}
\right]^{\mathbf{T}} \;.\end{displaymath}](img45.gif) |
(20) |
Additional special cases are presented in Appendix A.





Next: Example 1 - 2-D
Up: Acoustic wave-equation in 3D
Previous: One-way wavefield extrapolation
Stanford Exploration Project
4/5/2006
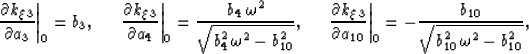
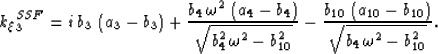
![]() . In addition, situations
exist where some coefficients are zero or negligible. For example,
the coefficients for a weakly non-orthogonal coordinate system
(i.e.
. In addition, situations
exist where some coefficients are zero or negligible. For example,
the coefficients for a weakly non-orthogonal coordinate system
(i.e. ![]() ) within a kinematic approximation reduce
to,
) within a kinematic approximation reduce
to,