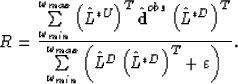Next: Related topics
Up: Wang and Shan: Imaging
Previous: migration imaging and inversion
At the scattering point, we can define a "distance" or norm as
| 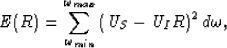 |
(39) |
where R is the reflectivity, 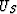 is the wavefield downward extrapolated to a reflector, and
is the wavefield downward extrapolated to a reflector, and 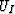 is the wavefield downward propagated to the reflector. The scattering wavefield
is the wavefield downward propagated to the reflector. The scattering wavefield 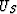 should be equal to or close to the convolution result between the wavefield
should be equal to or close to the convolution result between the wavefield 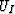 and the reflectivity.
Letting
and the reflectivity.
Letting
| 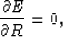 |
(40) |
we have
| 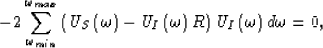 |
(41) |
If the incident wavefield equals zero, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is satisfied. However this case has no physical meaning. If the incident wavefield does not equal zero, then,
) is satisfied. However this case has no physical meaning. If the incident wavefield does not equal zero, then,
| 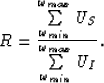 |
(42) |
In the complex domain, we can rewrite equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
| 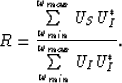 |
(43) |
If the incident wave is quite weak, the following regularization should be introduced:
| 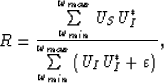 |
(44) |
where  is the regularization coefficient.
In fact, the reflectivity is related to the incident angle to a reflector of the plane-wave component of a seismic wave. Therefore, we should modify equation (
is the regularization coefficient.
In fact, the reflectivity is related to the incident angle to a reflector of the plane-wave component of a seismic wave. Therefore, we should modify equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into the following form to reach the angle gathers:
) into the following form to reach the angle gathers:
| 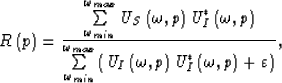 |
(45) |
where 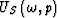 and
and 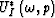 are a scattering plane wavefield and an incident plane wavefield, respectively.
In fact, the extrapolated wavefield can be defined as
are a scattering plane wavefield and an incident plane wavefield, respectively.
In fact, the extrapolated wavefield can be defined as
| 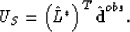 |
(46) |
Therefore, in the frequency domain, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as
| 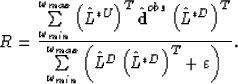 |
(47) |
We will further discuss this topic later to clarify the relationship.





Next: Related topics
Up: Wang and Shan: Imaging
Previous: migration imaging and inversion
Stanford Exploration Project
5/3/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is satisfied. However this case has no physical meaning. If the incident wavefield does not equal zero, then,
) is satisfied. However this case has no physical meaning. If the incident wavefield does not equal zero, then,
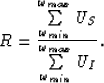
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
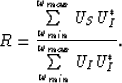
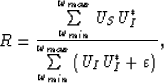
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into the following form to reach the angle gathers:
) into the following form to reach the angle gathers:
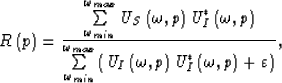
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be rewritten as
) can be rewritten as