Next: Wavefield extrapolation operator
Up: Shan and Biondi: 3D
Previous: Introduction
In 3D VTI media, the phase velocity of P- and SV-waves in Thomsen's notation can be expressed as follows Tsvankin (1996):
| 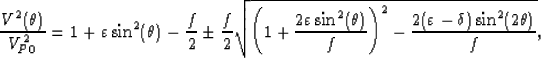 |
(1) |
where 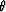 is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are
the P- and SV- wave velocities in the vertical direction, respectively.
The anisotropy parameters
is the phase angle of the propagating wave, and f=1-(VS0/VP0)2. VP0 and VS0 are
the P- and SV- wave velocities in the vertical direction, respectively.
The anisotropy parameters  and
and 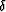 are defined by Thomsen (1986):
are defined by Thomsen (1986):
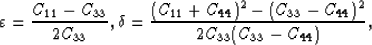
where Cij are elastic moduli.
In equation (1), 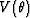 is the P-wave phase-velocity when the sign in front of the square root is positive,
and the SV-wave phase velocity for a negative sign. Let
is the P-wave phase-velocity when the sign in front of the square root is positive,
and the SV-wave phase velocity for a negative sign. Let 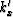 ,
, 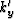 and
and 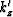 be the
wavenumbers for VTI media in Cartesian coordinates.
For plane-wave propagation, the phase angle
be the
wavenumbers for VTI media in Cartesian coordinates.
For plane-wave propagation, the phase angle 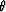 is related to
the wavenumbers
is related to
the wavenumbers 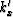 ,
, 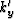 and
and 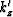 by the following relations:
by the following relations:
|  |
(2) |
where 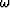 is the temporal frequency, and
is the temporal frequency, and 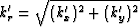 .From equations (1) and (2), we can derive the dispersion relation for 3D VTI media as follows:
.From equations (1) and (2), we can derive the dispersion relation for 3D VTI media as follows:
| 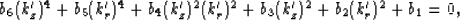 |
(3) |
where
| 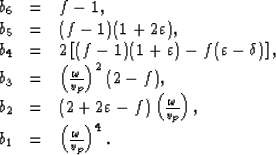 |
(4) |
For tilted TI media, the symmetry axis deviates from the vertical direction.
We need two angles to describe the tilting direction, the tilting angle 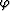 and the azimuth of the tilting direction
and the azimuth of the tilting direction 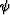 . We first assume
. We first assume 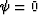 , that is the symmetry axis is in the plane y=0.
Then we generalize the dispersion relation to the case that
, that is the symmetry axis is in the plane y=0.
Then we generalize the dispersion relation to the case that 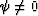 by coordinate rotation.
by coordinate rotation.
For a tilted TI medium, if we rotate the coordinates so that the symmetry axis is the axis 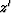 ,
it becomes a VTI medium in the new coordinates. Let kx, ky, and kz be the wavenumbers for
a tilted TI medium in Cartesian coordinates.
,
it becomes a VTI medium in the new coordinates. Let kx, ky, and kz be the wavenumbers for
a tilted TI medium in Cartesian coordinates. 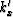 ,
, 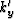 and
and 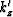 ,
which are the wavenumbers for VTI media in Cartesian coordinates, can also be considered as the wavenumbers
for tilted TI media in the rotated coordinates.
For the case that
,
which are the wavenumbers for VTI media in Cartesian coordinates, can also be considered as the wavenumbers
for tilted TI media in the rotated coordinates.
For the case that 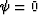 , the dispersion relation can be obtained from equation (3) by rotating the coordinates as follows:
, the dispersion relation can be obtained from equation (3) by rotating the coordinates as follows:
| 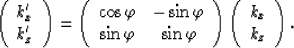 |
(5) |
We can re-organize the the dispersion relation and obtain the equation for the wavenumber kz
as follows:
|
a4kz4+a3kz3+a2kz2+a1kz+a0=0,
|
(6) |
where
| 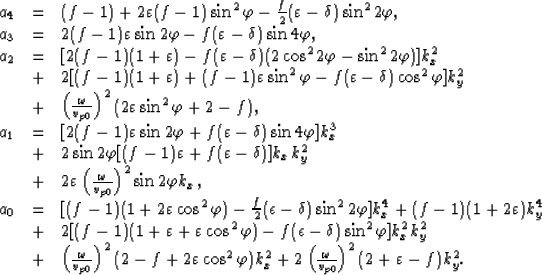 |
(7) |
Equation (6) is a quartic equation in kz. Given kx, kz, the velocity vp0, the anisotropy parameters
 and
and 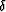 , and the tilting angle
, and the tilting angle 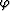 , we can calculate all the coefficients of equation (6),
and it can be solved analytically Abramowitz and Stegun (1972). Usually there are four solutions for equation (6). Two
of them are related to the up- and down-going P-wave, and the other two are related to the up- and down-going SV-wave, respectively.
, we can calculate all the coefficients of equation (6),
and it can be solved analytically Abramowitz and Stegun (1972). Usually there are four solutions for equation (6). Two
of them are related to the up- and down-going P-wave, and the other two are related to the up- and down-going SV-wave, respectively.
Let 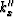 ,
, 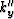 and
and 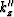 be the wavenumbers for tilted TI media with
a general
be the wavenumbers for tilted TI media with
a general 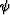 in the original coordinate system.
For general
in the original coordinate system.
For general 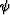 , after solving equation (6), we can get the wavenumber kz by rotating coordinates (kx,ky) as follows:
, after solving equation (6), we can get the wavenumber kz by rotating coordinates (kx,ky) as follows:
| 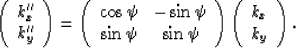 |
(8) |
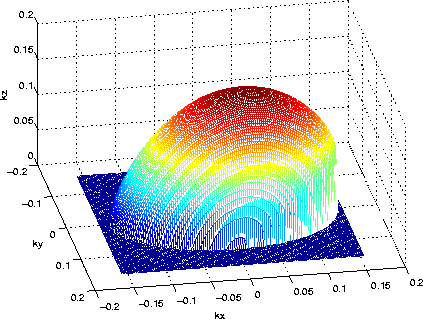
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows kz as a function of kx and ky in
a constant tilted TI medium. In this medium, the velocity is 2000 m/s,
shows kz as a function of kx and ky in
a constant tilted TI medium. In this medium, the velocity is 2000 m/s,
 is 0.4,
is 0.4, 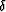 is 0.2,
is 0.2, 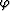 is
is 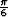 and
and 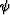 is 0.
The frequency used in Figure
is 0.
The frequency used in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) 57 Hz.
dispersion
57 Hz.
dispersion
Figure 1 Dispersion relation of 3D tilted TI media.






Next: Wavefield extrapolation operator
Up: Shan and Biondi: 3D
Previous: Introduction
Stanford Exploration Project
5/3/2005
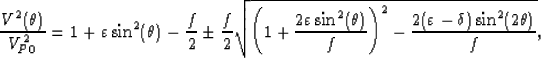
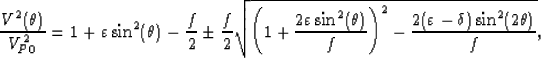
![]()
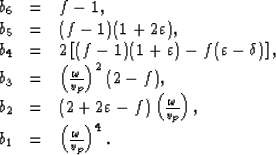
![]() ,
it becomes a VTI medium in the new coordinates. Let kx, ky, and kz be the wavenumbers for
a tilted TI medium in Cartesian coordinates.
,
it becomes a VTI medium in the new coordinates. Let kx, ky, and kz be the wavenumbers for
a tilted TI medium in Cartesian coordinates. ![]() ,
, ![]() and
and ![]() ,
which are the wavenumbers for VTI media in Cartesian coordinates, can also be considered as the wavenumbers
for tilted TI media in the rotated coordinates.
For the case that
,
which are the wavenumbers for VTI media in Cartesian coordinates, can also be considered as the wavenumbers
for tilted TI media in the rotated coordinates.
For the case that ![]() , the dispersion relation can be obtained from equation (3) by rotating the coordinates as follows:
, the dispersion relation can be obtained from equation (3) by rotating the coordinates as follows:
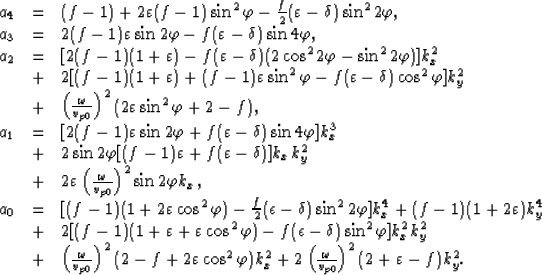
![]() ,
, ![]() and
and ![]() be the wavenumbers for tilted TI media with
a general
be the wavenumbers for tilted TI media with
a general ![]() in the original coordinate system.
For general
in the original coordinate system.
For general ![]() , after solving equation (6), we can get the wavenumber kz by rotating coordinates (kx,ky) as follows:
, after solving equation (6), we can get the wavenumber kz by rotating coordinates (kx,ky) as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows kz as a function of kx and ky in
a constant tilted TI medium. In this medium, the velocity is 2000 m/s,
shows kz as a function of kx and ky in
a constant tilted TI medium. In this medium, the velocity is 2000 m/s,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) 57 Hz.
57 Hz.