




Next: About this document ...
Up: Shan and Biondi: 3D
Previous: Acknowledgments
- Abramowitz, M., and Stegun, I., 1972, Solutions of quartic equations: New York: Dover., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 17-18.
-
- Baumstein, A., and Anderson, J., 2003, Wavefield extrapolation in laterally varying VTI media: Soc. of Expl. Geophys., 73rd Ann. Internat. Mtg., 945-948.
-
- Blacquiere, G., Debeye, H. W. J., Wapenaar, C. P. A., and Berkhout, A. J., 1989, 3D table-driven migration: Geophys. Prosp., 37, no. 08, 925-958.
-
- Ferguson, R. J., and Margrave, G. F., 1998, Depth migration in TI media by nonstationary phase shift: Soc. of Expl. Geophys., 68th Ann. Internat. Mtg, 1831-1834.
-
- Hale, D., 1991a, 3-D depth migration via McClellan transformations: Geophysics, 56, no. 11, 1778-1785.
-
- Hale, D., 1991b, Stable explicit depth extrapolation of seismic wavefields: Geophysics, 56, no. 11, 1770-1777.
-
- Holberg, O., 1988, Towards optimum one-way wave propagation: Geophys. Prosp., 36, no. 02, 99-114.
-
- McClellan, J., and Chan, D., 1977, A 2-D FIR filter structure derived from the Chebychev recursion: IEEE Trans. Circuits Syst.,, CAS-24, 372-378.
-
- McClellan, J. H., and Parks, T. W., 1972, Equiripple approximation of fan filters: Geophysics, 37, no. 04, 573-583.
-
- Ristow, D., and Ruhl, T., 1997, Migration in transversely isotropic media using implicit operators: Soc. of Expl. Geophys., 67th Ann. Internat. Mtg, 1699-1702.
-
- Rousseau, J. H. L., 1997, Depth migration in heterogeneous, transversely isotropic media with the phase-shift-plus-interpolation method: Soc. of Expl. Geophys., 67th Ann. Internat. Mtg, 1703-1706.
-
- Shan, G., and Biondi, B., 2004a, Imaging overturned waves by plane-wave migration in tilted coordinates: 74th Ann. Internat. Mtg., Soc. of Expl. Geophys., Expanded Abstracts, 969-972.
-
- Shan, G., and Biondi, B., 2004b, Wavefield extrapolation in laterally-varying tilted TI media: SEP-117, 1-10.
-
- Shan, G., and Biondi, B., 2005, Imaging steeply dipping reflectors in TI media by wavefield extrapolation: SEP-120, 63-76.
-
- Thomsen, L., 1986, Weak elastic anisotropy: Geophysics, 51, no. 10, 1954-1966.
-
- Thorbecke, J., 1997, Common focus point technology: Delft University of Technology., Ph.D. thesis.
-
- Tsvankin, I., 1996, P-wave signatures and notation for transversely isotropic media: An overview: Geophysics, 61, no. 02, 467-483.
-
- Uzcategui, O., 1995, 2-D depth migration in transversely isotropic media using explicit operators: Geophysics, 60, no. 06, 1819-1829.
-
- Zhang, J., Verschuur, D. J., and Wapenaar, C. P. A., 2001a, Depth migration of shot records in heterogeneous, tranversely isotropic media using optimum explicit operators: Geophys. Prosp., 49, no. 03, 287-299.
-
- Zhang, J., Wapenaar, C., and Verschuur, D., 2001b, 3-D depth migration in VTI media with explicit extrapolation operators: Soc. of Expl. Geophys., 71st Ann. Internat. Mtg, 1085-1088.
-
A
This appendix discusses how to estimate the coefficients aeenxny,
aoenxny, aeonxny and aoonxny in equations
(17)-(20).
We begin with equation (17), as the other three equations are silimiar.
Let 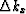 and
and 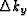 be the sampling of the wavenumbers kx
and ky, respectively. To mimic the behavior of the orginal operator
Fee,
we need to estimate aeenxny, so that
be the sampling of the wavenumbers kx
and ky, respectively. To mimic the behavior of the orginal operator
Fee,
we need to estimate aeenxny, so that
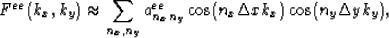
for ![$k_x\in [0,k_x^{{Nyquist}}]$](img58.gif) and
and
![$k_y\in [0,k_y^{{Nyquist}}]$](img59.gif) , where kxNyquist is the Nyquist wavenumber
, where kxNyquist is the Nyquist wavenumber
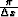 and kxNyquist is the Nyquist wavenumber
and kxNyquist is the Nyquist wavenumber 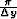 . Let Mx be
. Let Mx be 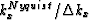 and My be
and My be
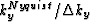 . The coefficients can be estimated by the
following fitting goals:
. The coefficients can be estimated by the
following fitting goals:
| 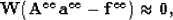 |
(30) |
where
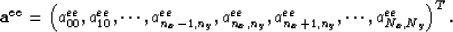
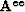 is a matrix with the elements
is a matrix with the elements
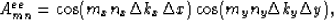
where m=my(Mx+1)+mx and n=ny(Nx+1)+nx.
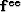 is a vector as follows
is a vector as follows
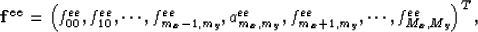
where 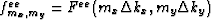 .
.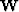 is a diagonal matrix with the weights for the wavenumbers kx,ky. High weights
are assigned to the wavenumbers of interest. The wavenumbers, such as the evacent energy,
are not of interest and are assigned low weights. Given the same weight matrix
is a diagonal matrix with the weights for the wavenumbers kx,ky. High weights
are assigned to the wavenumbers of interest. The wavenumbers, such as the evacent energy,
are not of interest and are assigned low weights. Given the same weight matrix 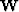 ,
the matrix
,
the matrix 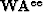 are same though fee changes with the function Fee(kx,ky).
Therefore, QR decomposition is a good way to solve the fitting goal (30). First,
we run QR decomposition on matrix
are same though fee changes with the function Fee(kx,ky).
Therefore, QR decomposition is a good way to solve the fitting goal (30). First,
we run QR decomposition on matrix 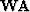 :
: 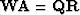 , where
, where 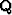 is an orthogonal matrix and
is an orthogonal matrix and 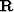 is an upper triangular matrix. We write down the matrixes
is an upper triangular matrix. We write down the matrixes 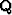 and
and 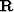 . Given the
function Fee(kx,ky), we caluculate
. Given the
function Fee(kx,ky), we caluculate 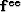 . The solution of fitting goal (30)
. The solution of fitting goal (30) 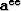 is given by
is given by
| 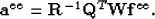 |
(31) |
For equation (18), we have the following fitting goal:
| 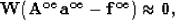 |
(32) |
where
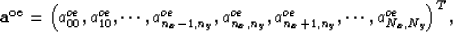
and 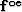 in equation (32) is
in equation (32) is
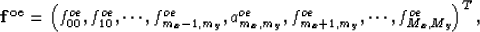
where 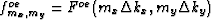 .
. 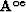 in equation (32)
is a matrix with the elements
in equation (32)
is a matrix with the elements
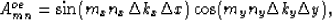
where m=my(Mx+1)+mx and n=ny(Nx+1)+nx.
For equation (19), we have the following fitting goal:
| 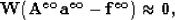 |
(33) |
where
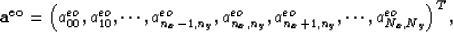
and 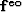 in equation (32) is
in equation (32) is
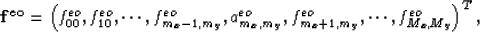
where 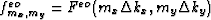 .
. 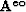 in equation (33)
is a matrix with the elements
in equation (33)
is a matrix with the elements
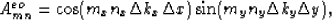
where m=my(Mx+1)+mx and n=ny(Nx+1)+nx.
For equation (20), we have the following fitting goal:
| 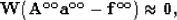 |
(34) |
where
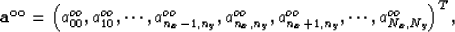
and 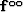 in equation (32) is
in equation (32) is
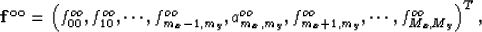
where 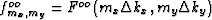 .
. 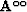 in equation (34)
is a matrix with the elements
in equation (34)
is a matrix with the elements
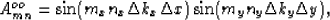
where m=my(Mx+1)+mx and n=ny(Nx+1)+nx.
Fitting goals (32), (33), and (34) can be solved in the same way as equation (30).
The solution of fitting goal (32), (33), (34) are given by
| 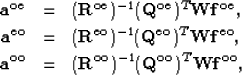 |
(35) |
| (36) |
| (37) |
where 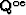 ,
, 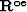 ,
, 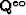 ,
, 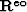 and
and 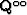 ,
, 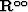 are the QR decomposition result of the matrixs
are the QR decomposition result of the matrixs 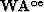 ,
, 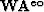 and
and 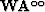 , respectively.
B
In this appendix, we derive the inverse Fourier transform of the correction operator F(kx,ky).
, respectively.
B
In this appendix, we derive the inverse Fourier transform of the correction operator F(kx,ky).
It is well known that the inverse Fourier transform of the function
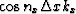 ,
, 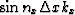 ,
, 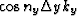 ,
, 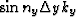 are:
are:
| 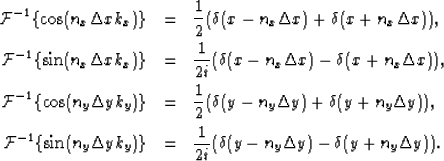 |
(38) |
| (39) |
| (40) |
| (41) |
Let 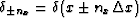 ,
, 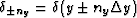 and
and
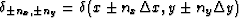 .The inverse Fourier transform of the function
.The inverse Fourier transform of the function 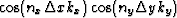 is :
is :
| 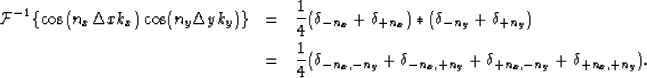 |
(42) |
| (43) |
Similarly, the inverse Fourier transform of the functions 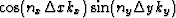 ,
,
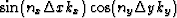 and
and 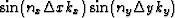 are :
are :
| 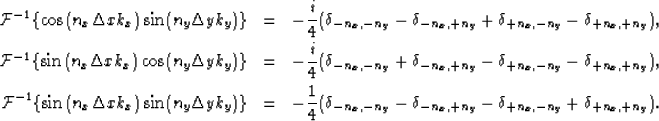 |
(44) |
| (45) |
| (46) |
Therefore the inverse Fourier transform of the functions Fee(kx,ky), Foe(kx,ky), Feo(kx,ky) and Foo(kx,ky) are:
| 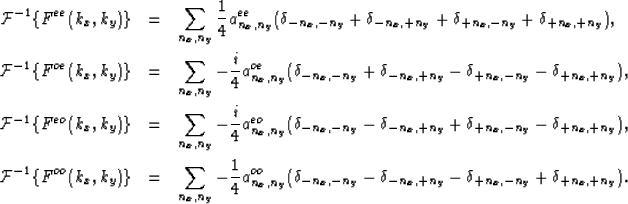 |
(47) |
| (48) |
| (49) |
| (50) |
The correction operator F(kx,ky) is the sum of Fee(kx,ky), Foe(kx,ky), Feo(kx,ky) and Foo(kx,ky).
Therefore the inverse Fourier transform of the correction operator is:
| 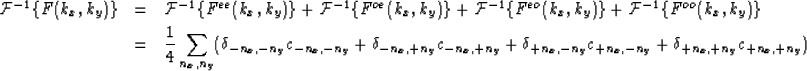 |
(51) |
| (52) |
where
| ![\begin{eqnarray}
c_{-n_x,-n_y}&=&[(a^{ee}_{n_x,n_y}-a^{oo}_{n_x,n_y})-i(a^{eo}_{...
...{n_x,n_y}-a^{oo}_{n_x,n_y})+i(a^{eo}_{n_x,n_y}+a^{oe}_{n_x,n_y})].\end{eqnarray}](img126.gif) |
(53) |
| (54) |
| (55) |
| (56) |





Next: About this document ...
Up: Shan and Biondi: 3D
Previous: Acknowledgments
Stanford Exploration Project
5/3/2005
![]() and
and ![]() be the sampling of the wavenumbers kx
and ky, respectively. To mimic the behavior of the orginal operator
Fee,
we need to estimate aeenxny, so that
be the sampling of the wavenumbers kx
and ky, respectively. To mimic the behavior of the orginal operator
Fee,
we need to estimate aeenxny, so that
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
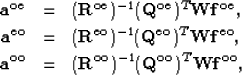
![]() ,
, ![]() ,
, ![]() ,
, ![]() are:
are:
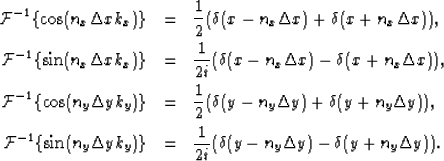
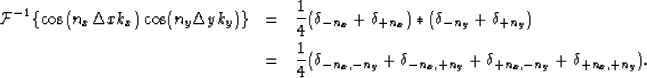
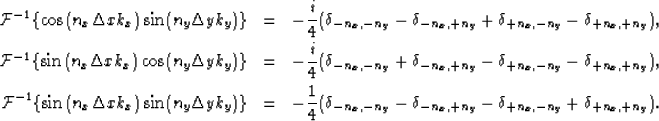
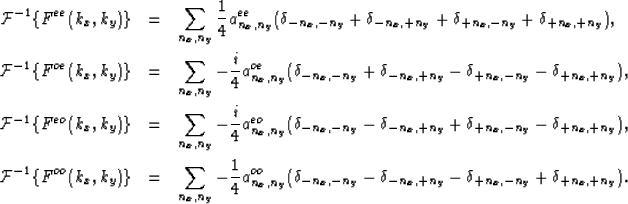
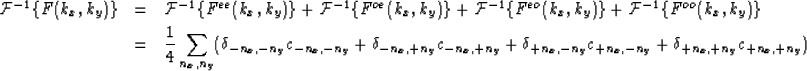
![\begin{eqnarray}
c_{-n_x,-n_y}&=&[(a^{ee}_{n_x,n_y}-a^{oo}_{n_x,n_y})-i(a^{eo}_{...
...{n_x,n_y}-a^{oo}_{n_x,n_y})+i(a^{eo}_{n_x,n_y}+a^{oe}_{n_x,n_y})].\end{eqnarray}](img126.gif)