Wavefield extrapolation operator

For a homogeneous medium, the wavefield can be extrapolated by an anisotropic phase shift in the Fourier domain as follows:

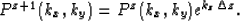$$P^{z+1}(k_x,k_y)=P^{z}(k_x,k_y)e^{k_z\Delta z}.$$ (9)

In reality, the velocity and anisotropy parameters change laterally. PSPI, explicit methods, or a combination of PSPI and explicit correction will remedy this problem. We extrapolate the wavefield by an isotropic operator with an explicit correction operator as follows:

$$P^{z+1}(k_x,k_y)=\left[ P^{z}(k_x,k_y)e^{k_z^{{iso}}\Delta z} \right ] e^{(k_z- k_z^{{iso}} )\Delta z}.$$ (10)

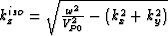where $k_z^{{iso}}=\sqrt{\frac{\omega^2}{V_{P0}^2}-(k_x^2+k_y^2)}$.In VTI media, the correction operator 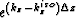$e^{(k_z- k_z^{{iso}} )\Delta z}$ is circularly symmetric. This allows us to use a 1D algorithm to replace the 2D operator by McClellan transformations Hale (1991a); McClellan and Chan (1977); McClellan and Parks (1972). However, tilting the symmetry axis in tilted TI media breaks the circular symmetry. As a result, we need to design a 2D convolution operator in the Fourier domain for wavefield extrapolation in 3D tilted TI media.

The correction operator is not symmetric for axes x or y in tilted TI media. This means

$$F(k_x,k_y)=e^{(k_z(k_x,k_y)-k_z^{{iso}})\Delta z}$$

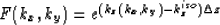
is not a even function of k_x and k_y. However, we can decompose the function F(k_x,k_y) into either even or odd functions of k_x and k_y, and approximate the even parts with cosine functions and the odd parts with sine functions.

We can decompose the function F(k_x,k_y) into even and odd parts for the axis k_x by

$$\begin{eqnarray} F^e(k_x,k_y)&=&\frac{1}{2}[F(k_x,k_y)+F(-k_x,k_y)],\\ F^o(k_x,k_y)&=&\frac{1}{2}[F(k_x,k_y)-F(-k_x,k_y)].\end{eqnarray}$$ (11) (12)

We can decompose the operator F^e and F^o into odd or even parts for the axis k_y by

$$\begin{eqnarray} F^{ee}(k_x,k_y)&=&\frac{1}{2}[F^e(k_x,k_y)+F^e(k_x,-k_y)],\\ F... ...y)],\\ F^{oo}(k_x,k_y)&=&\frac{1}{2}[F^o(k_x,k_y)-F^o(k_x,-k_y)].\end{eqnarray}$$ (13) (14) (15) (16)

The function F^ee(k_x,k_y) is an even function of both k_x and k_y, so it can be approximated by  

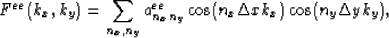$$F^{ee}(k_x,k_y)=\sum_{n_x,n_y}a^{ee}_{n_xn_y}\cos(n_x\Delta xk_x)\cos(n_y\Delta yk_y),$$ (17)

The function F^oe(k_x,k_y) is an even function of k_y and an odd function of k_x, so it can be approximated by  

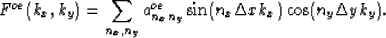$$F^{oe}(k_x,k_y)=\sum_{n_x,n_y}a^{oe}_{n_xn_y}\sin(n_x\Delta xk_x)\cos(n_y\Delta yk_y).$$ (18)

The function F^eo(k_x,k_y) is an even function of k_x and an odd function of k_y, so it can be approximated by  

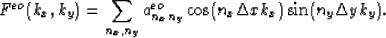$$F^{eo}(k_x,k_y)=\sum_{n_x,n_y}a^{eo}_{n_xn_y}\cos(n_x\Delta xk_x)\sin(n_y\Delta yk_y).$$ (19)

The function F^oo(k_x,k_y) is an odd function of both k_x,k_y, so it can be approximated by  

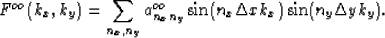$$F^{oo}(k_x,k_y)=\sum_{n_x,n_y}a^{oo}_{n_xn_y}\sin(n_x\Delta xk_x)\sin(n_y\Delta yk_y).$$ (20)

Coefficients a^ee_nxny, a^oe_nxny, a^eo_nxny and a^oo_nxny can be estimated by the weighted least-square method Thorbecke (1997), which can be solved by QR decomposition Baumstein and Anderson (2003); Shan and Biondi (2004b). Appendix A discusses how to estimate the coefficients a^ee_nxny, a^oe_nxny, a^eo_nxny and a^oo_nxny in detail.

The original operator F(k_x,k_y) can be obtained from F^ee(k_x,k_y), F^eo(k_x,k_y), F^oe(k_x,k_y) and F^oo(k_x,k_y) by

F(k_x,k_y)=F^ee(k_x,k_y)+F^eo(k_x,k_y)+F^oe(k_x,k_y)+F^oo(k_x,k_y).

Appendix B derives the inverse Fourier transform of the functions F^ee(k_x,k_y), F^eo(k_x,k_y), F^oe(k_x,k_y) and F^oo(k_x,k_y), and obtains the inverse Fourier transform of the function F(k_x,k_y) as follows:

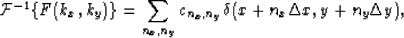$${\mathcal{F}}^{-1}\{ F(k_x,k_y)\}=\sum_{n_x,n_y}c_{n_x,n_y}\delta(x+n_x\Delta x, y+n_y\Delta y),$$ (22)

where

$$n_x=-N_x,-N_x+1,\cdots,-1,0,1,\cdots,N_x-1,N_x,$$

$$n_y=-N_y,-N_y+1,\cdots,-1,0,1,\cdots,N_y-1,N_y,$$

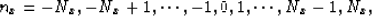
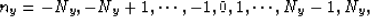
and c_nx,ny is as follows:

$$\begin{eqnarray} &&c_{00}=a^{ee}_{00},\\ &&c_{n_x,n_y}=\frac{1}{4}\left[ \left(... ...right) \right]. \ \ \ \ \ \ \ \mbox{if } n_x<0 \mbox{ and } n_y<0\end{eqnarray}$$ (23) (24) (25) (26) (27)

Let P^z(x,y) be the inverse Fourier transform of P^z(k_x,k_y). It is well known that

$$\delta(x+n_x\Delta x, y+n_y\Delta y)**P^z(x,y)=P^z(x+n_x\Delta x,y+n_y\Delta y),$$

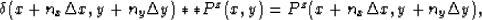
where ``**'' is 2D convolution. From the Fourier transform theory, we have

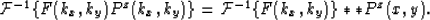$${\mathcal{F}}^{-1}\{ F(k_x,k_y)P^z(k_x,k_y)\}={\mathcal{F}}^{-1}\{ F(k_x,k_y)\}**P^z(x,y).$$ (28)

Therefore, we can apply the correction operator on the wavefield in the space domain as follows:

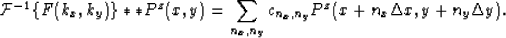$${\mathcal{F}}^{-1}\{ F(k_x,k_y)\}**P^z(x,y)=\sum_{n_x,n_y}c_{n_x,n_y}P^z(x+n_x\Delta x,y+n_y\Delta y).$$ (29)

From the above derivation, we know that the correction operator is designed in the Fourier domain and is implemented as a convolution in the space domain. For a laterally varying medium, we build a table of the convolution coefficients. When we run wavefield extrapolation, for each space position, we search for the corresponding convolution coefficients from that table and convolve the wavefield with these coefficients at that space position.