Angle gathers in the image-space

Angle gathers can be conveniently formed in the frequency-wavenumber domain using wavefield-continuation imaging methods. If we consider that in constant velocity media, t is the traveltime from the source to the reflector and back to the receiver at the surface, h is half the offset between the source and the receiver, z is the depth of the reflection point, $\alpha$ is the geologic dip, and $\gamma$ is the reflection angle (local), we can write  

$$\frac{\partial t}{\partial h} = \frac{2 \cos\alpha \sin\gamma }{v}$$ (21)

and  

$$\frac{\partial t}{\partial z} = \frac{2 \cos\alpha \cos\gamma }{v}.$$ (22)

From dtdh and dtdz, using the implicit functions theorem, we can write  

$$\tan{\gamma} = - \left. \frac{\partial z}{\partial h} \right\vert _ {t,x} ,$$ (23)

relation which is the basis for the angle gather method. The full derivation of freq is included in Appendix B.

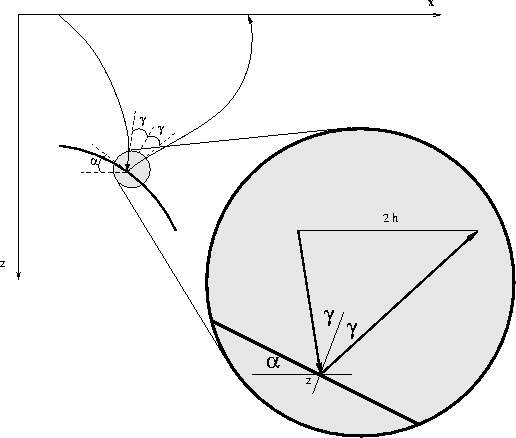
freq is derived in constant velocity media, but it remains perfectly valid in a differential sense in any arbitrary velocity media, if we consider h to be half the offset at the reflector depth. The offset at depth characterizes the downward-continued wavefield and, as local shows, this is the offset associated with the wavefield as it approaches the reflection surface and not the surface offset. In this context, the half-offset h can be seen as an image parameter, different from the offset at the surface which is a data parameter.

 

local
Figure 2 Reflection rays in an arbitrary-velocity medium.

In the frequency-wavenumber domain, formula () takes the simple form  

$$\tan \gamma = - \frac{k_h}{\kzz},$$ (24)

where $\kzz$ and k_h are the depth and frequency wavenumbers.

adcig indicates that angle gathers can be formed using frequency-domain algorithms. Wave-equation migration is ideally suited to compute angle gathers using such a method, since the migration output is precisely described by the offset at the reflector depth and not by the surface offset.

We can also recognize that dtdh simply describes the offset ray-parameter (p_h) of the propagating wave at the incidence with the reflector. Using the definition

$$p_h= \left. \frac{\partial t}{\partial h} \right\vert _ {z,x}$$ (25)

it follows that we can write a relation similar to adcig to evaluate the offset ray-parameter in the Fourier-domain:  

$$p_h=\frac{k_h}{\omega}.$$ (26)

Both adcig and pdcig can be used to compute image gathers through radial trace transforms in the Fourier domain (Appendix B). The major difference is that adcig operates in the image space, while pdcig operates in the data space.

Other major differences between the two methods are the following:

The image-space method is completely decoupled from migration, therefore conversion to reflection angle can be thought of as a post-processing after migration. Such post processing is useful because it allows conversion from the angle-domain back to the offset-domain without re-migration, a conclusion which does not hold true for the data-space method, where the transformation is a function of the data frequency. The transformation also allows for post-processing of the migrated images, e.g. angle gather anti-aliasing (8).

The angles we obtain using adcig are geometrical measures of the reflection angle. For AVA purposes, it is convenient to have the reflection amplitudes described as a function of reflection angle and not as a function of offset ray-parameter, in which case conversion to reflection angle requires dip and velocity information, as seen in dtdh. The meaning of the amplitude variation with angle in the ADCIGs created using this method depends on the properties of the migration algorithm from which the common image gathers are created (91). One of the following examples demonstrates that a correct implementation of this method can preserve the amplitude pattern resulting from migration.

Computing angle gathers in the image space requires acurate knowledge of velocity, since this gets encoded in the migrated image, and implicitly, in angle gathers. In contrast, the p_h gathers computed in the data space are insensitive to velocity inaccuracy, since the transformation only requires data space quantities. However, conversion of p_h to reflection angle $\gamma$is influenced by errors in the velocity maps (8).