




Next: Examples
Up: Angle-domain common image gathers
Previous: Angle gathers in the
The angle gather transformation introduced in this chapter
amounts to a stretch of the offset to reflection angle according
to adcig.
The stretch takes every point on the offset wavenumber axis and repositions
it on the angle axis, most likely not on a regular grid.
Therefore,
we need to interpolate the unevenly sampled axis to the regular one,
i.e. we need to solve a simple linear interpolation problem
| 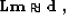 |
(27) |
where the model ( ) is represented by the evenly-spaced values on the
angle axis, the data (
) is represented by the evenly-spaced values on the
angle axis, the data (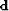 ) is represented by the unevenly-spaced values
on the angle axis, and
) is represented by the unevenly-spaced values
on the angle axis, and 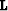 represents a 1D linear interpolation operator.
Both
represents a 1D linear interpolation operator.
Both  and
and 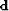 in interp are Fourier-domain quantities.
Since parts of the model space are not covered because of the uneven
distribution of the data, we need to regularize the interpolation process
and solve a system such as
in interp are Fourier-domain quantities.
Since parts of the model space are not covered because of the uneven
distribution of the data, we need to regularize the interpolation process
and solve a system such as
0
where (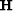 ) represents a 1D regularization operator
(1D gradient, for example).
The least-squares solution to the system (
) represents a 1D regularization operator
(1D gradient, for example).
The least-squares solution to the system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the usual
form
) takes the usual
form
| 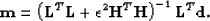 |
(28) |
In the special case of the angle-domain stretch, the inverted factor on
the right side of LSsol is a tridiagonal matrix
and can be easily inverted using a tridiagonal solver.
However, given the sparseness of the stretched data, the least-squares
tridiagonal matrix corresponding to the operator 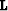 has zeros
present along the diagonals, which results in instability during
inversion and artifacts in the angle gathers.
Regularization fills those gaps and the inversion of the
matrix in LSsol is well-behaved.
has zeros
present along the diagonals, which results in instability during
inversion and artifacts in the angle gathers.
Regularization fills those gaps and the inversion of the
matrix in LSsol is well-behaved.
Finally, I emphasize that regularization is not applied in the
space domain, but in the Fourier domain and so
this method does not smooth reflection events spatially.
Consequently, the amplitude response in ADCIGs is not altered,
although, as noted earlier, there are
other reasons why direct AVA interpretation is not straightforward.





Next: Examples
Up: Angle-domain common image gathers
Previous: Angle gathers in the
Stanford Exploration Project
11/4/2004
![]() ) represents a 1D regularization operator
(1D gradient, for example).
The least-squares solution to the system (
) represents a 1D regularization operator
(1D gradient, for example).
The least-squares solution to the system (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the usual
form
) takes the usual
form
![]() has zeros
present along the diagonals, which results in instability during
inversion and artifacts in the angle gathers.
Regularization fills those gaps and the inversion of the
matrix in LSsol is well-behaved.
has zeros
present along the diagonals, which results in instability during
inversion and artifacts in the angle gathers.
Regularization fills those gaps and the inversion of the
matrix in LSsol is well-behaved.