Introduction

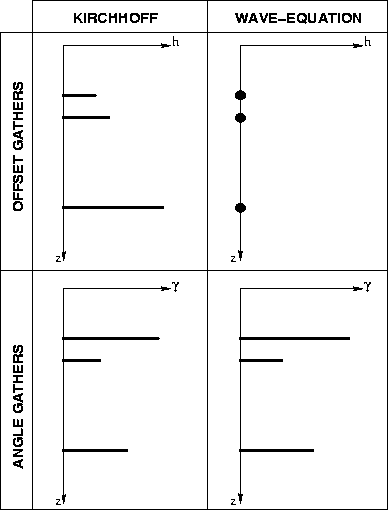Traditionally, migration velocity analysis and amplitude versus offset (AVO) studies employ offset-domain common image gathers (ODCIG), since most of the relevant information is not described by the zero-offset images. There are two kinds of ODCIGs: those produced by Kirchhoff migration, and those produced by migration by wavefield continuation, commonly referred to as wave-equation migration. These two kinds of ODCIGs have different meanings: for a perfectly known velocity model, the ODCIGs generated by Kirchhoff migration produce flat events, while the ODCIGs generated by wave-equation migration produce events perfectly focused at zero offset. There is no simple relationship between these two types of ODCIGs, as one involves the concept of flat gathers, while the other involves the concept of focused events. Furthermore, the offset used in the Kirchhoff ODCIGs is a data parameter, while the offset used in the wave-equation ODCIGs is a model parameter, since it characterizes the migrated image after focusing at the reflection point and not the recorded data.

Wave-equation migration is a powerful and accurate imaging tool in complex areas. However, offset-domain common image gathers fail to properly characterize complex propagation paths because, among other things, of the ambiguity of reflector positions caused by multipathing, which make interpretation and migration velocity analysis difficult (67).

The problems observed for ODCIGs can be alleviated using angle-domain common image gathers (ADCIG) which are representations of the seismic images sorted by the incidence angle at the reflection point. ADCIGs can be produced either by Kirchhoff methods (118; 16) or by wave-equation methods (17; 61; 75). Unlike ODCIGs, ADCIGs produced with either kind of method have similar characteristics since they simply describe the reflectivity as a function of incidence angle at the reflector (odcig). However, (101) argue that even in perfectly known but strongly refracting media, Kirchhoff ADCIGs are hampered by significant artifacts caused by the asymptotic assumptions of ray-based imaging.

 

odcig Figure 1 Offset-domain and angle-domain common image gathers. A schematic comparison between Kirchhoff and wave-equation methods.

This section focuses on ADCIGs computed in relation with wave-equation migration. Angle gathers can be obtained using wave-equation techniques either for shot-profile migration, as described by (17), or for shot-geophone migration, as described by (75) or (61). In both cases, angle gathers are evaluated using slant-stacks of the downward-continued wavefield, prior to imaging. I refer to these techniques as data-space methods since they involve the downward-continued wavefield before imaging. These data-space methods produce angle gathers as a function of offset ray-parameter (p_h), instead of the true reflection angle.

Here, I present an alternative method that enables us to compute angle gathers after imaging. I refer to this technique as an image-space method since it does not involve the wavefields anymore, but the prestack images obtained by imaging at zero time but not at zero offset. I show that this method directly produces angle gathers as a function of the reflection angle, as opposed to the data-space methods which produce angle gathers as a function of offset ray-parameter. The image-space method allows for a convenient, robust and slightly more efficient implementation than the data-space method. I also show that for both the data-space and image-space methods, the slant-stack transformation can be easily implemented as a radial-trace transform in the frequency-wavenumber domain, as described by (69).