




Next: LSJIMP: Choice of Imaging
Up: The LSJIMP Inverse problem
Previous: The LSJIMP Inverse problem
The LSJIMP method seeks to optimize the primary and multiple images,  ,
by minimizing the
,
by minimizing the 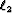 norm of the data residual, defined as the difference
between the recorded data,
norm of the data residual, defined as the difference
between the recorded data, 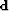 , and the modeled data,
, and the modeled data, 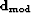 [equation (
[equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]:
)]:
| 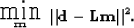 |
(4) |
Minimization (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is under-determined, for many choices of
prestack imaging operator, which implies an infinite number of
least-squares-optimal solutions. Practically speaking, this problem manifests
itself as crosstalk leakage. If (for instance)
) is under-determined, for many choices of
prestack imaging operator, which implies an infinite number of
least-squares-optimal solutions. Practically speaking, this problem manifests
itself as crosstalk leakage. If (for instance) 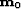 contains residual
first-order pegleg multiple energy, equation (
contains residual
first-order pegleg multiple energy, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will map
this energy back into data space, at the position of a first-order multiple.
Minimization (
) will map
this energy back into data space, at the position of a first-order multiple.
Minimization (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) alone cannot distinguish between crosstalk
and signal.
) alone cannot distinguish between crosstalk
and signal.
Of this infinity of possible  's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In section
's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In section
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I introduce model regularization operators to accomplish
both goals.
I introduce model regularization operators to accomplish
both goals.
After the minimization of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), theory dictates that
the data residual should be independent and identically distributed (iid), or
more intuitively, uncorrelated and evenly scaled. Correlated events in the
residual imply that the forward model,
), theory dictates that
the data residual should be independent and identically distributed (iid), or
more intuitively, uncorrelated and evenly scaled. Correlated events in the
residual imply that the forward model, 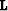 , poorly models or fails to model
events in the data. Examples of poor scaling might be the loss of reflection
strength for deep reflectors, or empty traces. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator,
, poorly models or fails to model
events in the data. Examples of poor scaling might be the loss of reflection
strength for deep reflectors, or empty traces. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator, 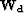 :
:
| ![\begin{displaymath}
\mbox{ \raisebox{-1.0ex}{ $\stackrel{\textstyle \mbox{\LARGE...
...ert {\bf W_d} \left[ \bold d - \bold L \bold m \right] \Vert^2,\end{displaymath}](img25.gif) |
(5) |
where strictly speaking,
| ![\begin{displaymath}
\left( {\bf W_d}^T {\bf W_d} \right)^{-1} = {\rm cov}[\bold d],\end{displaymath}](img26.gif) |
(6) |
although in my implementation of LSJIMP, outlined in section
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a far simpler choice for
, a far simpler choice for 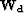 is used.
is used.





Next: LSJIMP: Choice of Imaging
Up: The LSJIMP Inverse problem
Previous: The LSJIMP Inverse problem
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]:
)]:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is under-determined, for many choices of
prestack imaging operator, which implies an infinite number of
least-squares-optimal solutions. Practically speaking, this problem manifests
itself as crosstalk leakage. If (for instance)
) is under-determined, for many choices of
prestack imaging operator, which implies an infinite number of
least-squares-optimal solutions. Practically speaking, this problem manifests
itself as crosstalk leakage. If (for instance) ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will map
this energy back into data space, at the position of a first-order multiple.
Minimization (
) will map
this energy back into data space, at the position of a first-order multiple.
Minimization (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) alone cannot distinguish between crosstalk
and signal.
) alone cannot distinguish between crosstalk
and signal.
![]() 's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In section
's, we seek the one which not only fits the
recorded data, but which also has minimum crosstalk leakage and maximum
consistency between signal events on different images. In section
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) I introduce model regularization operators to accomplish
both goals.
I introduce model regularization operators to accomplish
both goals.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), theory dictates that
the data residual should be independent and identically distributed (iid), or
more intuitively, uncorrelated and evenly scaled. Correlated events in the
residual imply that the forward model,
), theory dictates that
the data residual should be independent and identically distributed (iid), or
more intuitively, uncorrelated and evenly scaled. Correlated events in the
residual imply that the forward model, ![]() , poorly models or fails to model
events in the data. Examples of poor scaling might be the loss of reflection
strength for deep reflectors, or empty traces. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator,
, poorly models or fails to model
events in the data. Examples of poor scaling might be the loss of reflection
strength for deep reflectors, or empty traces. In general we compensate for a
correlated or poorly scaled data residual by adding a residual weighting
operator, ![]() :
:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , a far simpler choice for
, a far simpler choice for