




Next: Regularization 1: Differencing between
Up: The LSJIMP Inverse problem
Previous: LSJIMP: Choice of Imaging
In Sections ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I exploit three
discriminants between crosstalk and signal to devise model regularization
operators. The raw LSJIMP minimization [equation (
, I exploit three
discriminants between crosstalk and signal to devise model regularization
operators. The raw LSJIMP minimization [equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )] suffers
from non-uniqueness. The model regularization operators choose the particular
set of primary and multiple images which are optimally free of crosstalk, from an
infinite number of possible combinations. Moreover, these operators exploit
signal multiplicity-within and between images-to increase signal fidelity and
fill illumination gaps/missing traces. Some existing regularized least-squares
prestack migration schemes exploit signal multiplicity across reflection angle
Kuehl and Sacchi (2001); Prucha and Biondi (2002); Wang et al. (2003). LSJIMP's
additional use of multiples to regularize the least-squares imaging problem is
novel.
)] suffers
from non-uniqueness. The model regularization operators choose the particular
set of primary and multiple images which are optimally free of crosstalk, from an
infinite number of possible combinations. Moreover, these operators exploit
signal multiplicity-within and between images-to increase signal fidelity and
fill illumination gaps/missing traces. Some existing regularized least-squares
prestack migration schemes exploit signal multiplicity across reflection angle
Kuehl and Sacchi (2001); Prucha and Biondi (2002); Wang et al. (2003). LSJIMP's
additional use of multiples to regularize the least-squares imaging problem is
novel.
As mentioned in the previous section, my particular implementation of LSJIMP
processes each CMP location independently. Therefore, without loss of
generality, the regularization terms described in the following sections assume
that the prestack multiple images, 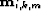 , are functions of
zero-offset traveltime (
, are functions of
zero-offset traveltime ( ) and offset (x), but not of midpoint. The same
logic applies to an image parameterized by depth and reflection angle.
) and offset (x), but not of midpoint. The same
logic applies to an image parameterized by depth and reflection angle.





Next: Regularization 1: Differencing between
Up: The LSJIMP Inverse problem
Previous: LSJIMP: Choice of Imaging
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I exploit three
discriminants between crosstalk and signal to devise model regularization
operators. The raw LSJIMP minimization [equation (
, I exploit three
discriminants between crosstalk and signal to devise model regularization
operators. The raw LSJIMP minimization [equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )] suffers
from non-uniqueness. The model regularization operators choose the particular
set of primary and multiple images which are optimally free of crosstalk, from an
infinite number of possible combinations. Moreover, these operators exploit
signal multiplicity-within and between images-to increase signal fidelity and
fill illumination gaps/missing traces. Some existing regularized least-squares
prestack migration schemes exploit signal multiplicity across reflection angle
Kuehl and Sacchi (2001); Prucha and Biondi (2002); Wang et al. (2003). LSJIMP's
additional use of multiples to regularize the least-squares imaging problem is
novel.
)] suffers
from non-uniqueness. The model regularization operators choose the particular
set of primary and multiple images which are optimally free of crosstalk, from an
infinite number of possible combinations. Moreover, these operators exploit
signal multiplicity-within and between images-to increase signal fidelity and
fill illumination gaps/missing traces. Some existing regularized least-squares
prestack migration schemes exploit signal multiplicity across reflection angle
Kuehl and Sacchi (2001); Prucha and Biondi (2002); Wang et al. (2003). LSJIMP's
additional use of multiples to regularize the least-squares imaging problem is
novel.