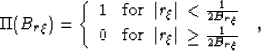Next: Downward continuation with the
Up: REFERENCES
Previous: Lattice basis of seismic
In a seismic experiment, measurements are necessarily acquired at
discrete sampling intervals.
This fact requires placing a restriction on the frequency content
representable on the 4-D lattice. One convenient manner to do this is to
apply a 4-D Rect function in the frequency domain to cut off
frequencies greater than predefined values
[e.g. 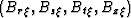 ].
To accomplish this, equation (7) is first Fourier transformed
over all variables to yield,
].
To accomplish this, equation (7) is first Fourier transformed
over all variables to yield,
| 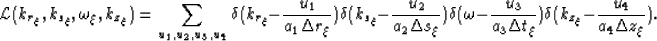 |
(8) |
A 4D Rect function, 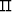 , with arguments (in 1D)
is then applied to the infinite Fourier domain lattice
, with arguments (in 1D)
is then applied to the infinite Fourier domain lattice 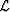 to yield a
band-limited version
to yield a
band-limited version 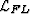 ,
,
| 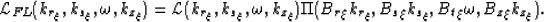 |
(9) |
Applying an inverse Fourier transform over all 4 dimensions to lattice
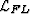 yields,
yields,
| 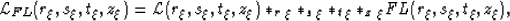 |
(10) |
where
|  |
(11) |
and the subscripts on the convolution symbol,  , delimit the
coordinate over which the convolution is applied.
Thus the seismic wavefield may be represented by,
, delimit the
coordinate over which the convolution is applied.
Thus the seismic wavefield may be represented by,
| 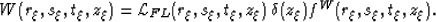 |
(12) |
It is important to emphasize that the lattice 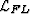 in
equation (13) represents only the lattice structure on
which the data wavefield is overlaid. For individual seismic
experiments, the values at each location will vary, while the lattice
structure remains invariant. Utilizing the crystal structure analogy
again, any atom may inhabit a node in the lattice, but there must be
one and only one atom present.
in
equation (13) represents only the lattice structure on
which the data wavefield is overlaid. For individual seismic
experiments, the values at each location will vary, while the lattice
structure remains invariant. Utilizing the crystal structure analogy
again, any atom may inhabit a node in the lattice, but there must be
one and only one atom present.





Next: Downward continuation with the
Up: REFERENCES
Previous: Lattice basis of seismic
Stanford Exploration Project
5/23/2004