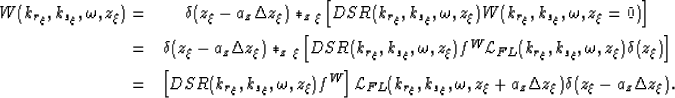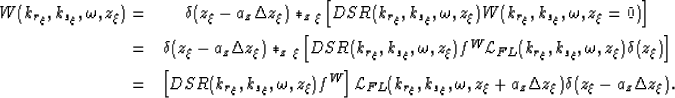Next: Evaluation of imaging condition
Up: REFERENCES
Previous: Band-limited lattices
In this section we apply the double square root (DSR) operator to
extrapolate the recorded wavefield of equation (13)
through the depth coordinate of the lattice. After initially Fourier
transforming the wavefield into 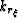 ,
, 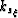 , and
, and 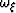 , the first
application of the DSR yields a new wavefield at depth step
, the first
application of the DSR yields a new wavefield at depth step
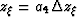 . Mathematically, this is represented by:
. Mathematically, this is represented by:
| 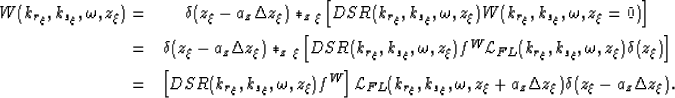 |
(13) |
| |
| |
The periodicity of the lattice over depth coordinate 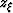 enables the
Shah function index uz to be shifted by
enables the
Shah function index uz to be shifted by 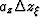 such that equation
(14) reads,
such that equation
(14) reads,
| 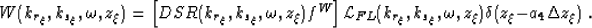 |
(14) |
By extension, any continuation step operating on a wavefield will take the same
form.
Applying an inverse Fourier transform over coordinates 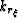 and
and 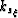 yields,
yields,
| ![\begin{displaymath}
W(\r,s_{\xi},\omega,z_{\xi}=a_4\Delta z_{\xi})=H(\r,s_{\xi},...
...\r,s_{\xi},\omega,z_{\xi})\d(z_{\xi}-a_4\Delta z_{\xi})\right] \end{displaymath}](img48.gif) |
(15) |
where , for convenience, H is defined by,
| ![\begin{displaymath}
H(\r,s_{\xi},\omega,z_{\xi})={\cal F}^{-1}_{k_{r_{\xi}},k_{s...
...}\left[DSR(k_{r_{\xi}},k_{s_{\xi}},\omega,z_{\xi})f^W\right]\;,\end{displaymath}](img49.gif) |
(16) |
where 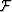 is the Fourier transform operator.
It is important to note here that the convolution of lattice
is the Fourier transform operator.
It is important to note here that the convolution of lattice 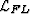 with filter H does not change the location of the sample points.
Rather, it operates only on the amplitudes at the predefined locations.
with filter H does not change the location of the sample points.
Rather, it operates only on the amplitudes at the predefined locations.





Next: Evaluation of imaging condition
Up: REFERENCES
Previous: Band-limited lattices
Stanford Exploration Project
5/23/2004