




Next: Band-limited lattices
Up: REFERENCES
Previous: REFERENCES
We choose to represent a seismic wavefield, W, by dissociating the
underlying interpolated acquisition lattice (IAL), 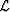 , from the discretely
sampled values of the continuous wavefield, fW.
Lattice
, from the discretely
sampled values of the continuous wavefield, fW.
Lattice 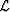 is defined over experimental source and receiver
coordinates,
is defined over experimental source and receiver
coordinates, 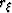 and
and 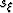 , and time and depth coordinates,
, and time and depth coordinates, 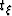 and
and 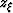 .
Importantly, the underlying grid function is only a construct of the
experimental process and is associated, accordingly, with
model space coordinates
.
Importantly, the underlying grid function is only a construct of the
experimental process and is associated, accordingly, with
model space coordinates 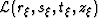 .This stands in contrast to the continuous wavefield
function defined by corresponding continuous variables, fW(r,s,t,z).
Written in this manner, it becomes natural to associate the act of
observation with the mapping from physical (continuous) to
experimental (discrete) variables,
.This stands in contrast to the continuous wavefield
function defined by corresponding continuous variables, fW(r,s,t,z).
Written in this manner, it becomes natural to associate the act of
observation with the mapping from physical (continuous) to
experimental (discrete) variables,
| 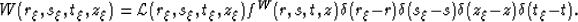 |
(6) |
Note, that we define W as the entire experimental wavefield
including traces from all source and receiver pairs. This volume is
separable into many different subsets, but we will keep it in tact.
One way to represent lattice 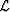 is with a 4D infinite
sum over delta functions (i.e. a 4D Shah function),
is with a 4D infinite
sum over delta functions (i.e. a 4D Shah function),
| 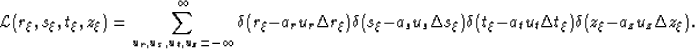 |
(7) |
In equation (7), variables (ar,as,at,az) are
subsampling factors over the fundamental discretization intervals
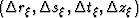 , and (ur,us,ut,uz) are the associated
summation indicies of the delta functions.
It is assumed that for our ideal grid
, and (ur,us,ut,uz) are the associated
summation indicies of the delta functions.
It is assumed that for our ideal grid 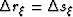 and any
departures from this equality may be represented through the subsampling
factors.
Throughout the development, unless specified otherwise, the summation from
and any
departures from this equality may be represented through the subsampling
factors.
Throughout the development, unless specified otherwise, the summation from 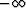 to
to 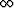 in equation (7) is assumed. Due to the fact
that no experiment is ever carried out with infinite extent, padding
the wavefields to infinity with zero traces maintains the rigor of
this evaluation.
in equation (7) is assumed. Due to the fact
that no experiment is ever carried out with infinite extent, padding
the wavefields to infinity with zero traces maintains the rigor of
this evaluation.





Next: Band-limited lattices
Up: REFERENCES
Previous: REFERENCES
Stanford Exploration Project
5/23/2004