




Next: Attenuation of multiples with
Up: Theory of multiple attenuation
Previous: Multiple attenuation
The PEFs are time-space domain non-stationary
filters to cope with the variability of seismic data
with time, offset and shot position. The basic equations for
non-stationary PEFs estimation are Guitton (2003b):
| 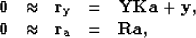 |
(8) |
where 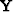 is a non-stationary combination matrix Margrave (1998),
is a non-stationary combination matrix Margrave (1998),
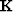 is a masking operator,
is a masking operator,  a vector
of the unknown PEFs coefficients,
a vector
of the unknown PEFs coefficients, 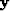 the data vector from which
we want to estimate the PEFs and
the data vector from which
we want to estimate the PEFs and 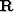 a regularization operator.
a regularization operator.
Often with seismic data, the amplitude varies across offset, midpoint and
time. These amplitude variations can be troublesome with
least-squares inversion because they tend to bias the final result
Claerbout (1992). Therefore, it is important to make sure that these amplitude
variations do not affect our processing. One solution is to apply a
weight to the data like Automatic Gain Control (AGC) or a geometrical
spreading correction. However, a better way is to incorporate this
weight inside the inversion by scaling the residual
Guitton (2003a). Introducing a weighting function 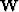 in the PEFs estimation leads to:
in the PEFs estimation leads to:
| 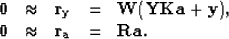 |
(9) |
As shown by Guitton (2003a), this weighting improves
the signal/noise separation results and can incorporate a mute zone
where no PEFs are to be estimated.
This weight can be different for the noise and the signal
PEFs. Estimating  in a least-squares sense
gives:
in a least-squares sense
gives:
| 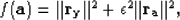 |
(10) |
which leads to the least-squares estimate of 
| 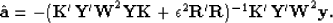 |
(11) |
Because many filter coefficients are estimated,  is
estimated iteratively with a conjugate-gradient method.
is
estimated iteratively with a conjugate-gradient method.
Now, prior to the signal estimation in equation (5),
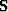 and
and 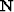 need to be computed from a signal and noise
model, respectively. The multiple model is often
(but not necessarily) derived by auto-convolving the recorded data
Verschhur et al. (1992), thus obtaining a prestack model of the multiples
later used to estimate a bank of non-stationary PEFs
need to be computed from a signal and noise
model, respectively. The multiple model is often
(but not necessarily) derived by auto-convolving the recorded data
Verschhur et al. (1992), thus obtaining a prestack model of the multiples
later used to estimate a bank of non-stationary PEFs 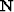 .
.
At this stage, a key assumption is that the relative amplitude
of all order of multiples is preserved.
In theory, an accurate surface-related multiple model can be derived
if (1) the source wavelet is known, (2) the surface
coverage is large enough, and (3) all the terms of the
Taylor series that model different orders of multiples
are incorporated Verschhur et al. (1992). In practice, however, a single
convolution is performed (first term of the Taylor series)
which gives a multiple model with erroneous
relative amplitude for high-order multiples
Guitton et al. (2001); Wang and Levin (1994).
In addition, the surface coverage might not be sufficient. This
can generate wrong amplitudes for short offset traces and
complex structures. Because PEFs estimate patterns, wrong
relative amplitude can affect the noise estimation. However, as we
shall see later, 3D filters seem to better cope with noise modeling
inadequacies.
The signal PEFs are more difficult to estimate since the signal
is usually unknown. However, Spitz (1999) shows
that for uncorrelated signal and noise, the data PEFs 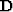 can be
approximated with
can be
approximated with
| 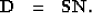 |
(12) |
As demonstrated by Claerbout and Fomel (2000), equation
(12) is a good approximation for the data PEFs
because PEFs are important where they are small. Both 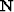 and
and
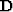 can be estimated from the model of the multiples and the data
(primaries plus multiples), respectively. Estimation of the signal PEFs
involves a deconvolution in equation (12) that can
be unstable with non-stationary filters. To avoid the deconvolution
step, the noise PEFs are convolved with the data:
can be estimated from the model of the multiples and the data
(primaries plus multiples), respectively. Estimation of the signal PEFs
involves a deconvolution in equation (12) that can
be unstable with non-stationary filters. To avoid the deconvolution
step, the noise PEFs are convolved with the data:
| 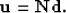 |
(13) |
Then the PEFs 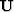 are estimated for
are estimated for 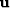 such that
such that
| 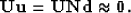 |
(14) |
From Spitz's approximation in equation (12), the
following relationships hold:
| 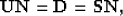 |
(15) |
and 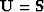 . Therefore, by convolving the data with the noise
PEFs, signal PEFs consistent with the Spitz approximation can be computed.
Equation (12) insures that the PEFs
. Therefore, by convolving the data with the noise
PEFs, signal PEFs consistent with the Spitz approximation can be computed.
Equation (12) insures that the PEFs 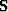 and
and
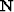 will not span similar components
of the data space.
will not span similar components
of the data space.
Thanks to the Helix Claerbout (1998); Mersereau and Dudgeon (1974), the
PEFs can have any dimension. In this paper, I use 2D and 3D
filters and demonstrate that 3D filters lead to the best noise attenuation
result. When 2D filters are used, the multiple attenuation is
performed on one shot gather at a time. When 3D filters are used,
the multiple attenuation is performed on one macro-gather at a
time. A macro-gather is a cube made of fifty consecutive shots
with all the offsets and time samples. When the multiple attenuation
is done, the macro-gathers are reassembled to form the final result.
There is an overlap of five shots between successive macro-gathers.
In the next section, I show a prestack multiple attenuation
example with the synthetic Sigsbee2B dataset.
stratigraphy
Figure 1 Stratigraphic interval velocity model of the Sigsbee2B
dataset.
 datasignal
datasignal
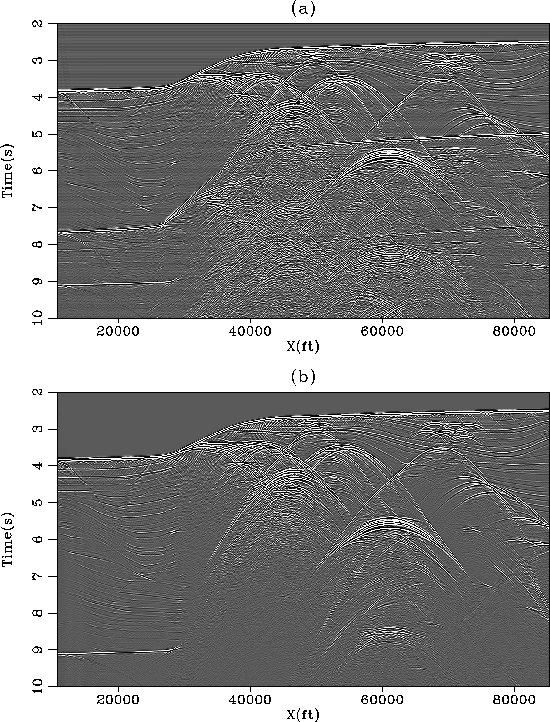
Figure 2 Two constant offset sections (h=1125 ft)
of the Sigsbee2B dataset with (a) and without (b) free surface
condition. The multiples are very strong below 5 s.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)






Next: Attenuation of multiples with
Up: Theory of multiple attenuation
Previous: Multiple attenuation
Stanford Exploration Project
5/23/2004
![]() in the PEFs estimation leads to:
in the PEFs estimation leads to:
![]() and
and ![]() need to be computed from a signal and noise
model, respectively. The multiple model is often
(but not necessarily) derived by auto-convolving the recorded data
Verschhur et al. (1992), thus obtaining a prestack model of the multiples
later used to estimate a bank of non-stationary PEFs
need to be computed from a signal and noise
model, respectively. The multiple model is often
(but not necessarily) derived by auto-convolving the recorded data
Verschhur et al. (1992), thus obtaining a prestack model of the multiples
later used to estimate a bank of non-stationary PEFs ![]() .
.![]() can be
approximated with
can be
approximated with

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)