Attenuation of multiples with the Sigsbee2B dataset

The Sigsbee2B dataset was designed to generate strong surface-related multiples. Figure 1 shows the true stratigraphic interval velocity model for this dataset. The data were created with a 2D acoustic finite difference modeler with constant density. Two datasets were generated: one with a free surface (Figure 2a) and one without a free surface (Figure 2b). These two datasets are such that a direct subtraction of the two leads to an almost true prestack model of the surface-related multiples. Because this multiple attenuation technique deals with the subtraction step only, the multiple model obtained by subtraction of the two datasets with and without free-surface conditions is used for the noise PEFs estimation for all my computations.

As stated in the introduction, I focus my analysis in the image space after migration. In complex geology, multiple attenuation results should always be assessed after migration; the effects of the multiple attenuation technique on the amplitudes of the primaries in ADCIGs (e.g., Figure 3), or on migrated images at zero offset (e.g., Figure 4) can be then directly assessed. For the Sigsbee2B dataset, a split-step double square-root (DSR) migration code with three reference velocities is used.

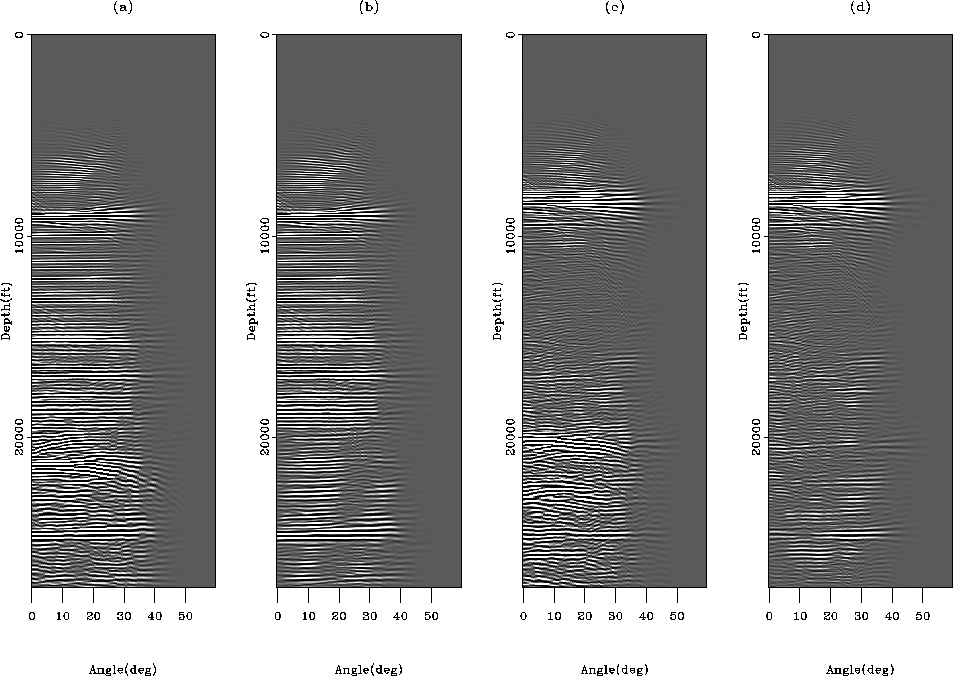
Ideally, because the data were created with finite differences, a finite differences migration code should be used to take the full complexity of the wave propagation into account. Figure 3d illustrates the limits of the migration algorithm by showing non-flat events below the salt. In contrast, Figure 3b displays flat gathers in the sedimentary section left of the salt body. An illumination effect is clearly visible below 20,000 ft, between 20 and 30 deg in Figure 3b. Figures 3a and 3c highlight the effects of the multiples on ADCIG by creating numerous artifacts and fictitious events.

It is interesting and somewhat surprising to see that in Figure 4a the multiples are very weak after migration below the salt compared to the constant offset sections in Figure 2a. In particular, the water bottom multiple seems to disappear. This is because the multiples are extremely distorted by the migration process in the vicinity of the complex salt structure. Compared with the migration of the primaries only in Figure 4b, the multiples in Figure 4a are masking a lot of primaries in the deepest part of the model and thus need to be removed.

 

datasignal2-ang
Figure 3 ADCIGs for the migrated data at two different surface locations inside (i.e., 33 kft) and outside (i.e., 30 kft) the salt boundaries. (a) ADCIG at 30 kft for the data with multiples. (b) ADCIG at 30 kft for the data without multiples. (c) ADCIG at 33 kft for the data with multiples. (d) ADCIG at 33 kft for the data without multiples. Theoretically, with the appropriate migration algorithm, this last gather should be flat everywhere.

 

datasignal-mig
Figure 4 Migrated images at zero-offset for the data with (a) and without (b) free surface condition. Comparing with Figure 2, the multiples appear much weaker below the salt after migration. However, some reflectors near 22 kft are hidden in (a).

In the next section, I demonstrate that in the ideal case where a model for both the primaries and multiples exist, the primaries can be recovered with almost no bias from the attenuation technique. Then, without any model for the primaries, I show that the Spitz approximation gives an excellent multiple attenuation result when 3D filters are used.

 

• Estimating biases
• Testing the Spitz approximation