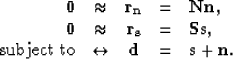Next: Filter estimation
Up: Theory of multiple attenuation
Previous: Theory of multiple attenuation
First consider that any seismic data 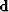 are the sum of signal (primaries) and
noise (multiples) as follows:
are the sum of signal (primaries) and
noise (multiples) as follows:
|  |
(1) |
where  is the signal we want to
preserve and
is the signal we want to
preserve and 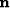 the noise we wish to attenuate.
the noise we wish to attenuate.
Now assuming that the multidimensional PEFs 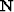 and
and 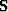 are known for the noise and signal components, respectively (see the following section for
a complete description of the PEFs estimation step), we have
are known for the noise and signal components, respectively (see the following section for
a complete description of the PEFs estimation step), we have
| 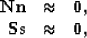 |
(2) |
by definition of the PEFs. Equations (1) and (2) can
be combined to solve a constrained problem to separate signal from
noise as follows:
| 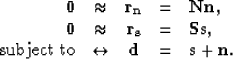 |
(3) |
The noise 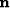 can be eliminated in the last equation of the fitting goal
(3) by convolving with
can be eliminated in the last equation of the fitting goal
(3) by convolving with 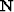 . Doing so, equation
(3) becomes:
. Doing so, equation
(3) becomes:
| 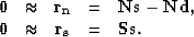 |
(4) |
Sometimes it is useful to add a masking operator on
the noise and signal residuals 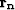 and
and 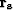 when performing
the noise attenuation. It happens for example when we want to isolate
and preserve parts of the data where no multiples are present. For
instance, a mute zone can be taken into account very easily.
Calling
when performing
the noise attenuation. It happens for example when we want to isolate
and preserve parts of the data where no multiples are present. For
instance, a mute zone can be taken into account very easily.
Calling 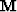 this masking operator, the fitting goals
in equation (4) are weighted as follows:
this masking operator, the fitting goals
in equation (4) are weighted as follows:
| 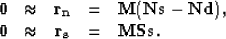 |
(5) |
Solving for  in a least-squares sense leads to the objective
function
in a least-squares sense leads to the objective
function
| 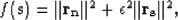 |
(6) |
where  is a trade-off parameter that relates to
the signal/noise ratio. The
least-squares inverse for
is a trade-off parameter that relates to
the signal/noise ratio. The
least-squares inverse for  becomes
becomes
| 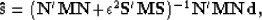 |
(7) |
where (') stands for the adjoint. Soubaras (1994) uses a
very similar approach for random noise attenuation and more recently
for coherent noise attenuation Soubaras (2001) with F-X PEFs.
Because the size of the data space can be quite large,
 is estimated iteratively with a conjugate-gradient method.
In the next section, I describe how both
is estimated iteratively with a conjugate-gradient method.
In the next section, I describe how both 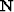 and
and 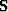 are estimated.
are estimated.





Next: Filter estimation
Up: Theory of multiple attenuation
Previous: Theory of multiple attenuation
Stanford Exploration Project
5/23/2004
![]() and
and ![]() are known for the noise and signal components, respectively (see the following section for
a complete description of the PEFs estimation step), we have
are known for the noise and signal components, respectively (see the following section for
a complete description of the PEFs estimation step), we have