Finite-difference solutions to the one-way wave equation

Alternative solutions to the one-way wave-equation are represented by pure finite-difference methods in the $\omega-x$ domain, which can be implemented either as implicit Claerbout (1985), or as explicit methods Hale (1991). For the same stencil size, the implicit methods are more accurate and robust than explicit methods, although harder to implement, particularly in 3-D. However, explicit methods of comparable accuracy can be designed using larger stencils.

For the implicit methods, various approximations to the square root in equation (12) lead to approximate equations of various orders of accuracy. In the Cartesian space, those methods are known by their respective angular accuracy as the $15^\circ$ equation, $45^\circ$ equation and so on. Although the meanings of $15^\circ$, $45^\circ$ are undefined in ray coordinates where the extrapolation axis is time, we can still write approximations for the numerical finite-difference solutions using analogous approximations.

If we introduce the notation

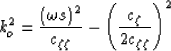$$\; k_o^2 = \frac{\left(\omega\ss\right)^2}{\c_{\zeta\zeta}} - \left(\frac{\c_{\zeta}}{2\c_{\zeta\zeta}}\right)^2$$ (19)

we can simplify the one-way wave equation (12) as  

$$k_\zeta= i \frac{\c_{\zeta}}{2\c_{\zeta\zeta}} + \sqrt{ \; k... ...right] - \frac{\c_{\xi\eta}}{\c_{\zeta\zeta}} k_\xi k_\eta }\;.$$ (20)

 

• $15^\circ$ wave-equation in a 3-D Riemannian space