




Next: Mixed-domain solutions to the
Up: Sava and Fomel: Riemannian
Previous: Acoustic wave-equation in 3-D
Equation (6) can be used to describe
two-way propagation of acoustic waves in a semi-orthogonal
Riemannian space.
For one-way wavefield extrapolation, we need to modify
the acoustic wave equation (6) by selecting a single
direction of propagation.
In order to simplify the computations,
we introduce the following notation:
| ![\begin{eqnarray}
\c_{\zeta\zeta}&=& \frac{1 }{\AA^2} \;, \nonumber \\ \c_{\xi\xi...
...{\partial } {\partial \xi } \left(F\frac{\AA}{J}\right) \right]\;.\end{eqnarray}](img37.gif) |
|
| |
| |
| |
| |
| |
| (8) |
All quantities in equations (8)
can be computed by finite-differences for any choice of
a Riemannian coordinate system
which fulfills the orthogonality condition indicated earlier.
In particular, we can use ray coordinates to compute those
coefficients. With these notations, the acoustic wave-equation
can be written as:
| 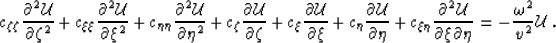 |
(9) |
For the particular case of Cartesian coordinates
(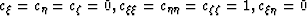 ),
the Helmholtz equation (9) takes the familiar form
),
the Helmholtz equation (9) takes the familiar form
| 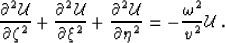 |
(10) |
From equation (9), we can directly
deduce the modified form
of the dispersion relation for the wave-equation in a
semi-orthogonal 3-D Riemannian space:
| 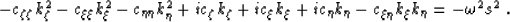 |
(11) |
For one-way wavefield extrapolation, we need to solve
the second order equation (11)
for the wavenumber of the extrapolation direction 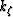 ,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
,and select the solution with the appropriate sign to
extrapolate waves in the desired direction:
| ![\begin{displaymath}
k_\zeta= i \frac{\c_{\zeta}}{2\c_{\zeta\zeta}} \pm
\sqrt{
\f...
...right]
- \frac{\c_{\xi\eta}}{\c_{\zeta\zeta}} k_\xi k_\eta
}\;.\end{displaymath}](img43.gif) |
(12) |
The solution with the positive sign in equation (12) corresponds to
propagation in the positive direction of the extrapolation axis 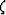 .
.
For the particular case of Cartesian coordinates
(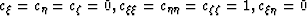 ),
the one-way wavefield extrapolation equation takes the
familiar form
),
the one-way wavefield extrapolation equation takes the
familiar form
| 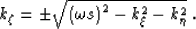 |
(13) |





Next: Mixed-domain solutions to the
Up: Sava and Fomel: Riemannian
Previous: Acoustic wave-equation in 3-D
Stanford Exploration Project
10/14/2003
![\begin{eqnarray}
\c_{\zeta\zeta}&=& \frac{1 }{\AA^2} \;, \nonumber \\ \c_{\xi\xi...
...{\partial } {\partial \xi } \left(F\frac{\AA}{J}\right) \right]\;.\end{eqnarray}](img37.gif)
![\begin{eqnarray}
\c_{\zeta\zeta}&=& \frac{1 }{\AA^2} \;, \nonumber \\ \c_{\xi\xi...
...{\partial } {\partial \xi } \left(F\frac{\AA}{J}\right) \right]\;.\end{eqnarray}](img37.gif)
![\begin{displaymath}
k_\zeta= i \frac{\c_{\zeta}}{2\c_{\zeta\zeta}} \pm
\sqrt{
\f...
...right]
- \frac{\c_{\xi\eta}}{\c_{\zeta\zeta}} k_\xi k_\eta
}\;.\end{displaymath}](img43.gif)
![]() ),
the one-way wavefield extrapolation equation takes the
familiar form
),
the one-way wavefield extrapolation equation takes the
familiar form