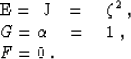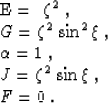Next: One-way wave-equation in 3-D
Up: Sava and Fomel: Riemannian
Previous: Introduction
The Laplacian operator of a scalar function 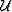 in an arbitrary
Riemannian space with coordinates
in an arbitrary
Riemannian space with coordinates 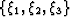 has the form
has the form
| 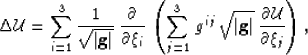 |
(1) |
where gij is a component of the associated metric tensor,
and 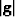 is its determinant Synge and Schild (1978).
is its determinant Synge and Schild (1978).
The expression simplifies if one of the coordinates
(e.g. the coordinate of one-way wave extrapolation)
is orthogonal to the other coordinates. Let 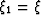 ,
,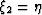 , and
, and 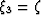 ,
with
,
with 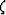 orthogonal to both
orthogonal to both 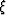 and
and  .
Then the metric tensor has the matrix
.
Then the metric tensor has the matrix
| ![\begin{displaymath}
\left[g_{ij}\right] = \left[\begin{array}
{ccc}
E& F& 0 \\ F& G& 0 \\ 0 & 0 & \AA^2
\end{array}\right]\;,\end{displaymath}](img12.gif) |
(2) |
where E, F, G, and  are differential forms that can be found
from mapping Cartesian coordinates
are differential forms that can be found
from mapping Cartesian coordinates  to the general coordinates
to the general coordinates
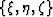 , as follows:
, as follows:
| 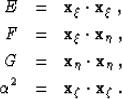 |
|
| |
| |
| (3) |
The associated metric tensor has the matrix
| ![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
+G/J^2 & ...
... -F/J^2 & +E/J^2 & 0 \\ 0 & 0 & 1/\AA^2
\end{array}\right]\;,\end{displaymath}](img17.gif) |
(4) |
where 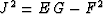 .
The metric determinant takes the form
.
The metric determinant takes the form
| 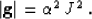 |
(5) |
Substituting equations (4) and (5) into
(1), we can modify the Helmholtz wave equation
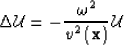
for propagating waves in a 3-D Riemannian space:
| ![\begin{eqnarray}
\frac{1}{\AA\,J}
\left[
\frac{\partial } {\partial \zeta } \lef...
...tial \xi }
\right)
\right]
= - \frac{\omega^2}{v^2} \mathcal{U}\;.\end{eqnarray}](img21.gif) |
(6) |
In equation (6),
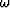 is temporal frequency,
is temporal frequency,
![$v\left[\bf{x}\left(\xi,\eta,\zeta\right)\right]$](img23.gif) is the wave propagation velocity, and
is the wave propagation velocity, and
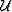 represents a propagating wave.
represents a propagating wave.
For the special case of two dimensional spaces
(F=0 and G=1),
the Helmholtz wave equation reduces to the simpler form:
| ![\begin{displaymath}
\frac{1}{\AA J}
\left[\frac{\partial } {\partial \zeta } \le...
...l \xi } \right) \right]
= - \frac{\omega^2}{v^2} \mathcal{U}\;,\end{displaymath}](img24.gif) |
(7) |
which corresponds to a curvilinear orthogonal coordinate system.
Particular examples of coordinate systems for one-way wave propagation are:
- Cartesian (propagation in depth):
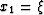 ,
, 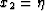 ,
, 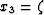 ,
,
- Cylindrical (propagation in radius):
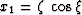 ,
, 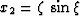 ,
, 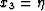 ,
,
- Spherical (propagation in radius):
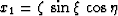 ,
, 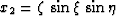 ,
, 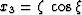 ,
,
- Ray family (propagation along rays):
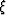 and
and  represent
parameters defining a particular ray in the family (i.e. the ray take-off
angles), J is the geometrical spreading factor, related to the
cross-sectional area of the ray tube Cervený (2001). The coefficients
E, F, G, and J are easily computed by
finite-difference approximations
with the Huygens wavefront tracing technique Sava and Fomel (2001). If
the propagation parameter
represent
parameters defining a particular ray in the family (i.e. the ray take-off
angles), J is the geometrical spreading factor, related to the
cross-sectional area of the ray tube Cervený (2001). The coefficients
E, F, G, and J are easily computed by
finite-difference approximations
with the Huygens wavefront tracing technique Sava and Fomel (2001). If
the propagation parameter 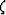 is taken to be time along the ray, then
is taken to be time along the ray, then
 equals the propagation velocity v.
equals the propagation velocity v.





Next: One-way wave-equation in 3-D
Up: Sava and Fomel: Riemannian
Previous: Introduction
Stanford Exploration Project
10/14/2003
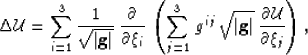
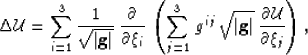
![]() ,
,![]() , and
, and ![]() ,
with
,
with ![]() orthogonal to both
orthogonal to both ![]() and
and ![]() .
Then the metric tensor has the matrix
.
Then the metric tensor has the matrix
![\begin{displaymath}
\left[g_{ij}\right] = \left[\begin{array}
{ccc}
E& F& 0 \\ F& G& 0 \\ 0 & 0 & \AA^2
\end{array}\right]\;,\end{displaymath}](img12.gif)
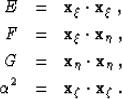
![\begin{displaymath}
\left[g^{ij}\right] =
\left[\begin{array}
{ccc}
+G/J^2 & ...
... -F/J^2 & +E/J^2 & 0 \\ 0 & 0 & 1/\AA^2
\end{array}\right]\;,\end{displaymath}](img17.gif)