




Next: Low-frequency limit of
Up: SQUIRT-FLOW MODEL
Previous: Squirt aij Coefficients
We next must obtain the coefficient 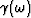 in the mesoscopic
transport law
in the mesoscopic
transport law 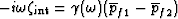 . Again, the approach is to first obtain the limiting
behaviour at low and high frequencies and then to connect the two limits
by a simple function.
. Again, the approach is to first obtain the limiting
behaviour at low and high frequencies and then to connect the two limits
by a simple function.
The fluid response in phase 1 (the principal porespace) is governed by
the Navier-Stokes equation 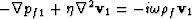 and the compressibility law
and the compressibility law  where
where 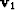 is the local fluid velocity in
the pores.
Since for all frequencies of interest
we have that
is the local fluid velocity in
the pores.
Since for all frequencies of interest
we have that 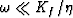 (note that
(note that 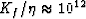 s-1 for liquids and
1010 s-1 for gases), the fluid pressure in phase 1 is governed
by the wave equation
s-1 for liquids and
1010 s-1 for gases), the fluid pressure in phase 1 is governed
by the wave equation
| 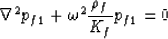 |
(96) |
and since the acoustic wavelength in the fluid is always much greater than
the grain sizes,
the fluid pressure in the principal porespace satisfies
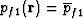 (a spatial constant) at all frequencies.
(a spatial constant) at all frequencies.
The focus, then, is on determining the flow and fluid pressure
within the cracked grains (phase 2) that is governed by the
local porous-continuum laws 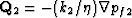 and
and
| 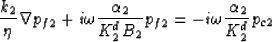 |
(97) |
where 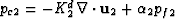 .
This deformation and pressure change is excited by applying a uniform
normal stress
.
This deformation and pressure change is excited by applying a uniform
normal stress 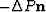 to the surface of the averaging volume
with the fluid pressure satisfying the
boundary conditions
to the surface of the averaging volume
with the fluid pressure satisfying the
boundary conditions
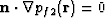 on
on 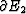 and
and
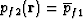 on
on 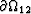 .
.
![]() and the compressibility law
and the compressibility law ![]() where
where ![]() is the local fluid velocity in
the pores.
Since for all frequencies of interest
we have that
is the local fluid velocity in
the pores.
Since for all frequencies of interest
we have that ![]() (note that
(note that ![]() s-1 for liquids and
1010 s-1 for gases), the fluid pressure in phase 1 is governed
by the wave equation
s-1 for liquids and
1010 s-1 for gases), the fluid pressure in phase 1 is governed
by the wave equation
![]() and
and