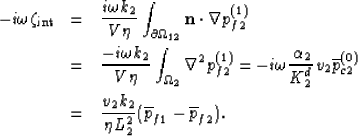Next: High-frequency limit of
Up: Squirt Transport
Previous: Squirt Transport
The fluid pressure and confining pressure
in the grains can again be developed as asymptotic series
in 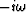 [as in equations (60)-(61)].
The zero-order response corresponds to the static limit in
which the fluid pressure is everywhere the same and given by
[as in equations (60)-(61)].
The zero-order response corresponds to the static limit in
which the fluid pressure is everywhere the same and given by
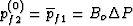 with
Bo = -(a12+a13)/(a22 + 2 a23 + a33) and with the
aij as given by equations (90)-(95).
The detailed result for Bo can be expressed
with
Bo = -(a12+a13)/(a22 + 2 a23 + a33) and with the
aij as given by equations (90)-(95).
The detailed result for Bo can be expressed
| ![\begin{eqnarray}
&&\frac{1/K-(1-\alpha_2)/K_2^d}{B_o}
= \frac{1}{K} - \frac{(1-\...
...right]
+ v_2 \frac{\alpha_2}{K_2^d} \left[\frac{1}{B_2} - 1\right]\end{eqnarray}](img186.gif) |
|
| (98) |
which reduces to the standard Gassmann expression given in the
appendix (with a total porosity given by 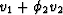 ) when
B2 and
) when
B2 and 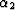 are themselves given by the Gassmann expressions.
In this same zero-order limit, the undrained bulk modulus
is defined as 1/Kou = a11 + (a12 + a13) Bo which also reduces to
the standard Gassmann expression when B2 and
are themselves given by the Gassmann expressions.
In this same zero-order limit, the undrained bulk modulus
is defined as 1/Kou = a11 + (a12 + a13) Bo which also reduces to
the standard Gassmann expression when B2 and 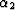 are
themselves given by Gassmann expressions.
are
themselves given by Gassmann expressions.
The leading-order in 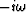 correction to uniform fluid pressure
is thus governed by the problem
correction to uniform fluid pressure
is thus governed by the problem
| 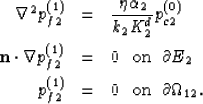 |
(99) |
| (100) |
| (101) |
Here, pc2(0) is the local confining pressure in the grain
space in the static limit that can be written
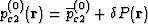 .
The average static confining pressure throughout the grains is
determined from equation (84) with
.
The average static confining pressure throughout the grains is
determined from equation (84) with 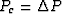 and
and
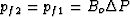 to yield
to yield
| 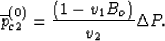 |
(102) |
The deviations 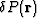 thus volume integrate to zero
thus volume integrate to zero
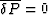 and
are formally defined
and
are formally defined
| 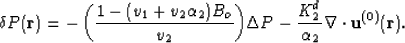 |
(103) |
The local perturbations 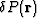 are thus highly sensitive to the detailed
nature of the grain packing and grain geometry. Fortunately, these perturbations
do not play an important role in the theory.
are thus highly sensitive to the detailed
nature of the grain packing and grain geometry. Fortunately, these perturbations
do not play an important role in the theory.
The fluid pressure in the grains is now written in the scaled
form
| 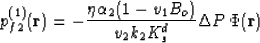 |
(104) |
where the potential 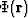 is independent of
is independent of 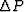 and
is a solution of the elliptic problem
and
is a solution of the elliptic problem
| 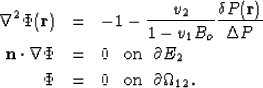 |
(105) |
| (106) |
| (107) |
To leading-order in 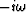 , an average of equation (104) gives
, an average of equation (104) gives
| 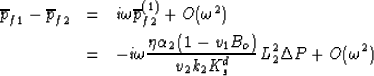 |
(108) |
| (109) |
where the squared length L22 is defined
| ![\begin{displaymath}
L_2^2 = \overline{\Phi} = \overline{\Phi}_o \left[
1 + \frac...
...\overline{\Phi_o \delta P}}{\overline{\Phi}_o \Delta P}
\right]\end{displaymath}](img200.gif) |
(110) |
with overlines denoting volume averages over the grain space and with
the potential 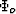 defined as the solution of
defined as the solution of
| 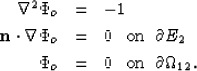 |
(111) |
| (112) |
| (113) |
Although it is not generally true that 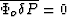 for all grain geometries, we nonetheless expect this integral to be small
because
for all grain geometries, we nonetheless expect this integral to be small
because 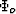 is a smooth function and
is a smooth function and 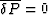 .
The local perturbations in the static confining pressure
.
The local perturbations in the static confining pressure
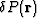 require a solution of the static displacements throughout
the entire grain space--a daunting numerical task. Whenever
the length L2 needs to be estimated, such as in the numerical
results that follow, our approach is to simply
use
the reasonable approximation that
require a solution of the static displacements throughout
the entire grain space--a daunting numerical task. Whenever
the length L2 needs to be estimated, such as in the numerical
results that follow, our approach is to simply
use
the reasonable approximation that
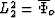 .
.
Last, from the definition 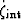 of the internal transfer
we have that to leading order in
of the internal transfer
we have that to leading order in 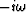
| 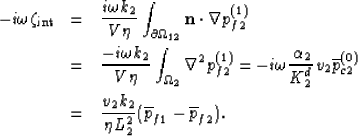 |
(114) |
| (115) |
| (116) |
The normal 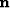 in equation (114) is outward to phase 1
which accounts for the sign change in equation(115). Note as
well that equation (115) is a volume average of equation (99)
while equation (116) follows from equations (102) and
(109).
The desired limit is thus
in equation (114) is outward to phase 1
which accounts for the sign change in equation(115). Note as
well that equation (115) is a volume average of equation (99)
while equation (116) follows from equations (102) and
(109).
The desired limit is thus
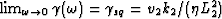 .
.





Next: High-frequency limit of
Up: Squirt Transport
Previous: Squirt Transport
Stanford Exploration Project
10/14/2003
![]() [as in equations (60)-(61)].
The zero-order response corresponds to the static limit in
which the fluid pressure is everywhere the same and given by
[as in equations (60)-(61)].
The zero-order response corresponds to the static limit in
which the fluid pressure is everywhere the same and given by
![]() with
Bo = -(a12+a13)/(a22 + 2 a23 + a33) and with the
aij as given by equations (90)-(95).
The detailed result for Bo can be expressed
with
Bo = -(a12+a13)/(a22 + 2 a23 + a33) and with the
aij as given by equations (90)-(95).
The detailed result for Bo can be expressed
![\begin{eqnarray}
&&\frac{1/K-(1-\alpha_2)/K_2^d}{B_o}
= \frac{1}{K} - \frac{(1-\...
...right]
+ v_2 \frac{\alpha_2}{K_2^d} \left[\frac{1}{B_2} - 1\right]\end{eqnarray}](img186.gif)
![]() correction to uniform fluid pressure
is thus governed by the problem
correction to uniform fluid pressure
is thus governed by the problem
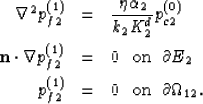
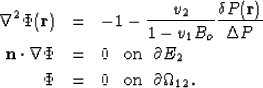
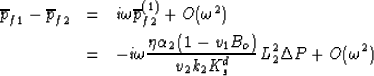
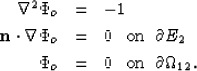
![]() of the internal transfer
we have that to leading order in
of the internal transfer
we have that to leading order in ![]()