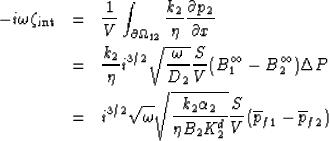Next: Full model for
Up: Squirt Transport
Previous: Low-frequency limit of
In the extreme high-frequency limit, the fluid has no time to
significantly escape
from the porous grains (phase 2) and enter the main porespace
(phase 1). As such, the fluid pressure distribution
in each phase is reasonably modeled as
| 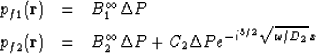 |
(117) |
| (118) |
where x is again a local coordinate measuring distance
normal to the interface  and where
D2 is the fluid-pressure diffusivity within the
porous grains that is given by
and where
D2 is the fluid-pressure diffusivity within the
porous grains that is given by 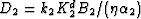 .
In reality, the local confining
pressure
.
In reality, the local confining
pressure 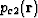 throughout the grains has spatial fluctuations
about the average value and we have made the approximation
that
throughout the grains has spatial fluctuations
about the average value and we have made the approximation
that 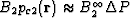 = the average fluid
pressure throughout the grain space. It is easy to demonstrate that
under undrained and unrelaxed conditions,
= the average fluid
pressure throughout the grain space. It is easy to demonstrate that
under undrained and unrelaxed conditions,
| 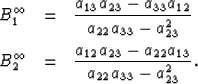 |
(119) |
| (120) |
Since these 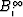 do not appear in the final result,
we do not bother substituting in the aij constants from
equations (90)-(95).
do not appear in the final result,
we do not bother substituting in the aij constants from
equations (90)-(95).
The continuity of fluid pressure pf2 = pf1 along 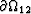 (x=0) requires that
(x=0) requires that 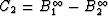 . The definition of
. The definition of
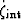 may now be used to write
may now be used to write
| 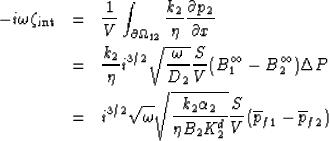 |
(121) |
| (122) |
| (123) |
where we have used, to leading order in the high-frequency limit, that
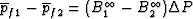 .
The desired limit is thus
.
The desired limit is thus
 .
.





Next: Full model for
Up: Squirt Transport
Previous: Low-frequency limit of
Stanford Exploration Project
10/14/2003
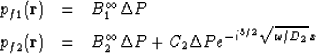
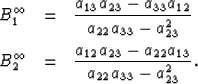
![]() (x=0) requires that
(x=0) requires that ![]() . The definition of
. The definition of
![]() may now be used to write
may now be used to write