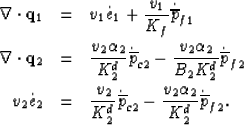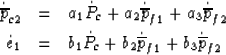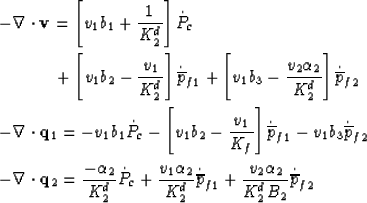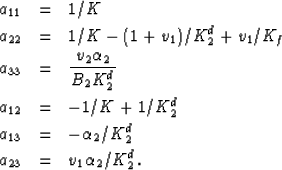Next: Squirt Transport
Up: SQUIRT-FLOW MODEL
Previous: SQUIRT-FLOW MODEL
To obtain the aij coefficients in the squirt model, we first note that
these coefficients are defined under conditions where 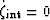 (no fluid passing between the porous grains and the principal porespace).
Under these conditions,
the rate of
fluid depletion
(no fluid passing between the porous grains and the principal porespace).
Under these conditions,
the rate of
fluid depletion 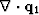 of a sample
(rate of fluid volume being extruded
from the principal pore space via
the exterior sample surface as normalized by the sample volume)
is due to the difference between the rate of dilatation of the principal
porespace (denoted here as
of a sample
(rate of fluid volume being extruded
from the principal pore space via
the exterior sample surface as normalized by the sample volume)
is due to the difference between the rate of dilatation of the principal
porespace (denoted here as 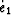 )
and the rate at which
fluid in the pores is dilating
)
and the rate at which
fluid in the pores is dilating 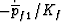 . If we
also perform a volume average of equation (3) over the porous grain space
and use the notation that
. If we
also perform a volume average of equation (3) over the porous grain space
and use the notation that
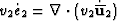 we obtain
the following three equations
we obtain
the following three equations
| 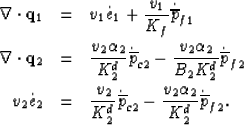 |
(81) |
| (82) |
| (83) |
The macroscopic dilatation of interest is 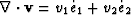 .
In order to obtain the macroscopic
compressibility laws for porous-grain/principal-porespace composite, we
introduce linear response laws of the form
.
In order to obtain the macroscopic
compressibility laws for porous-grain/principal-porespace composite, we
introduce linear response laws of the form
| 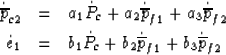 |
(84) |
| (85) |
where the ai and bi must be found.
We note immediately that from the definition
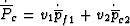 one has
one has
| 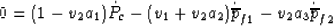 |
(86) |
which must hold true for any variation of the independent pressure variables so
that a1=1/v2, a2 = - v1/v2, a3 = 0.
To obtain the bi, we now
combine the above into the macroscopic laws
| 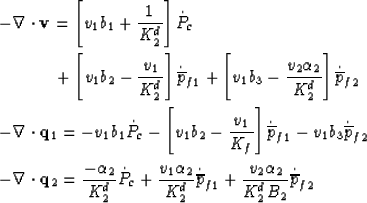 |
|
| (87) |
| (88) |
| (89) |
and use the fact that the coefficients of the matrix must be symmetric
(aij = aji). With a11 = 1/K corresponding to the overall
drained frame modulus of the composite (to be independently specified),
we obtain v1 b1 = 1/K - 1/K2d, v1 b2 = -1/K + (1+v1)/K2d,
and 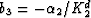 . The final aij coefficients are
exactly
. The final aij coefficients are
exactly
| 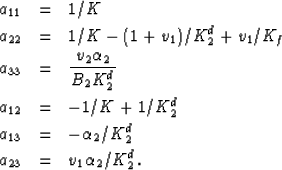 |
(90) |
| (91) |
| (92) |
| (93) |
| (94) |
| (95) |
Reasonable models for K and Kd2 will be discussed shortly.





Next: Squirt Transport
Up: SQUIRT-FLOW MODEL
Previous: SQUIRT-FLOW MODEL
Stanford Exploration Project
10/14/2003
![]() (no fluid passing between the porous grains and the principal porespace).
Under these conditions,
the rate of
fluid depletion
(no fluid passing between the porous grains and the principal porespace).
Under these conditions,
the rate of
fluid depletion ![]() of a sample
(rate of fluid volume being extruded
from the principal pore space via
the exterior sample surface as normalized by the sample volume)
is due to the difference between the rate of dilatation of the principal
porespace (denoted here as
of a sample
(rate of fluid volume being extruded
from the principal pore space via
the exterior sample surface as normalized by the sample volume)
is due to the difference between the rate of dilatation of the principal
porespace (denoted here as ![]() )
and the rate at which
fluid in the pores is dilating
)
and the rate at which
fluid in the pores is dilating ![]() . If we
also perform a volume average of equation (3) over the porous grain space
and use the notation that
. If we
also perform a volume average of equation (3) over the porous grain space
and use the notation that
![]() we obtain
the following three equations
we obtain
the following three equations