




Next: COMPUTED EXAMPLES
Up: INTERPRETATION OF P AND
Previous: General analysis for VTI
The analysis presented so far is general for all VTI elastic media.
But we can say more by assuming now that the anisotropy arises due to
layering. Then, for example, we have the following relations
| 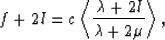 |
(57) |
| 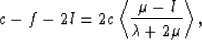 |
(58) |
and
| ![\begin{eqnarray}
a - f - 2l = 2c \left\{\left<{{2m-\mu -l}\over{\lambda + 2\mu}}...
...
- \left<{{\mu}\over{\lambda + 2\mu}}\right\gt^2\right]\right\}.
\end{eqnarray}](img117.gif) |
(59) |
Eq. (57) is an easy consequence of the Backus averaging
formulas.
Then, (58) shows that c differs from f + 2l only by a
term that measures the difference in the weighted average of 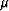 and
l. Eq. (59) shows that a differs from f + 2l
in a more complicated fashion that depends on the difference in the
weighted average of (2m-l) and
and
l. Eq. (59) shows that a differs from f + 2l
in a more complicated fashion that depends on the difference in the
weighted average of (2m-l) and 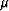 , as well as a term that is
higher order in the fluctuations of the layer
, as well as a term that is
higher order in the fluctuations of the layer 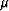 values.
Combining these results, we have
values.
Combining these results, we have
| ![\begin{eqnarray}
G_{eff} = m - {{4c}\over{3}}\left[\left<{{\mu^2}\over{\lambda +...
...right\gt
- \left<{{\mu}\over{\lambda + 2\mu}}\right\gt^2\right],
\end{eqnarray}](img118.gif) |
(60) |
showing that all the interesting behavior (including strong 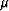 fluctuations in the layers together with
fluctuations in the layers together with 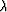 dependence) is
collected in Geff.
Since the product of (58) and (59) is clearly of
higher order in the fluctuations of the layer shear moduli, it is not
hard to see that, to leading order when these fluctuation effects are small,
dependence) is
collected in Geff.
Since the product of (58) and (59) is clearly of
higher order in the fluctuations of the layer shear moduli, it is not
hard to see that, to leading order when these fluctuation effects are small,
| 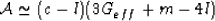 |
(61) |
from which we can conclude that the important coefficient in
(46) is given to a good approximation by
| 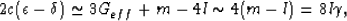 |
(62) |
where the final expression is a statement about the limiting behavior when
either the 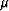 fluctuations are very small, or when strong undrained
behavior is present together with large
fluctuations are very small, or when strong undrained
behavior is present together with large 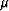 fluctuations.
fluctuations.
To study the fluid effects, the drained Lamé parameter 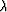 in
each layer should be replaced under undrained conditions by
in
each layer should be replaced under undrained conditions by
| 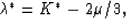 |
(63) |
where K* was defined by (6). Then, for small
fluctuations in 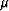 , Eq. (62) shows that the
leading order terms due to these shear modulus variations contributing
to
, Eq. (62) shows that the
leading order terms due to these shear modulus variations contributing
to 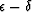 actually do not depend on the fluids at all
(since m-l does not depend on them).
There is an enhancement in the shear wave speed for SV in layered
media, just due to the changes in the shear moduli, and independent of any
fluids that might be present in that case, but the magnitude of this
enhancement is small because the difference m-l is also small. When
m-l is large, then the magnitude of the enhancement due to liquids
in the pores can be very substantial as we will see in the following examples.
So the effects of liquid on Geff will generally be weak when the
fluctuations in
actually do not depend on the fluids at all
(since m-l does not depend on them).
There is an enhancement in the shear wave speed for SV in layered
media, just due to the changes in the shear moduli, and independent of any
fluids that might be present in that case, but the magnitude of this
enhancement is small because the difference m-l is also small. When
m-l is large, then the magnitude of the enhancement due to liquids
in the pores can be very substantial as we will see in the following examples.
So the effects of liquid on Geff will generally be weak when the
fluctuations in 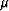 are weak, and strong when they are strong.
are weak, and strong when they are strong.
To check the corresponding result for P-waves, we need to estimate 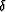 .Making use of (56), we also have
.Making use of (56), we also have
| ![\begin{eqnarray}
c\delta = -2c\left<{{\mu - l}\over{\lambda + 2\mu}}\right\gt
\l...
...ight\gt^{-1}
\left<{{\mu-l}\over{\lambda+2\mu}}\right\gt\right].
\end{eqnarray}](img122.gif) |
(64) |
Working to the same order as we did for the final expression in
(62), we can neglect the second term in the
square brackets of (64).
What remains shows that pore fluids would have an effect on this
result. The result is
| 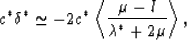 |
(65) |
and a similar replacement should also be made for Geff
in (60). Eq. (65) shows that,
since c* and 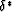 both depend on the
both depend on the 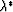 's (although
in opposite ways, since
one increases while the other decreases as
's (although
in opposite ways, since
one increases while the other decreases as 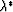 increases),
the product of these factors will have some dependence on fluids.
The degree to which fluctuations in
increases),
the product of these factors will have some dependence on fluids.
The degree to which fluctuations in 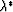 and
and 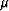 are
correlated or anticorrelated as they vary from layer to layer
will also affect these results in predictable ways.
are
correlated or anticorrelated as they vary from layer to layer
will also affect these results in predictable ways.
Now we have derived all the results needed to interpret
(34) and show how it is related to
(33). First, we note the some of the main terms
missing from (34) are
those due to approximations made to 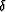 and the denominators
of (33), which have been approximated as
and the denominators
of (33), which have been approximated as
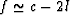 instead of
instead of 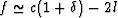 .Then, from (62), it is easy to see that
the final term in (34) vanishes to lowest
order, and that the remainder is given exactly by the shear modulus
fluctuation terms in brackets in (59) -- in complete agreement
with the final terms of (33). Then,
from (64), it follows that the leading
contribution to the factor
.Then, from (62), it is easy to see that
the final term in (34) vanishes to lowest
order, and that the remainder is given exactly by the shear modulus
fluctuation terms in brackets in (59) -- in complete agreement
with the final terms of (33). Then,
from (64), it follows that the leading
contribution to the factor 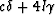 is
is
| 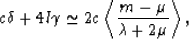 |
(66) |
in complete agreement with the second term in (33).
In the case of very strong fluctuations in the layer shear moduli,
then (59) and (64) both show that
effects of the pore fluids can be more strongly felt in the anisotropy
correction factors 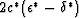 and
and 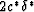 for undrained porous media, and therefore more easily observed in
seismic, sonic, or ultrasonic data. When these effects are present,
the vertically polarized quasi-shear mode will show the highest
magnitude effect, the horizontally polarized shear mode will show
no effect, and the quasi-compressional mode will show an effect of
intermediate magnitude. It is known that these effects, when present,
are always strongest at
for undrained porous media, and therefore more easily observed in
seismic, sonic, or ultrasonic data. When these effects are present,
the vertically polarized quasi-shear mode will show the highest
magnitude effect, the horizontally polarized shear mode will show
no effect, and the quasi-compressional mode will show an effect of
intermediate magnitude. It is known that these effects, when present,
are always strongest at 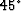 , and are diminished when the angle
of propagation is either
, and are diminished when the angle
of propagation is either 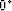 or
or 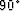 relative to the
layering direction. We will test these analytical predictions
with numerical examples in the next section.
relative to the
layering direction. We will test these analytical predictions
with numerical examples in the next section.
To summarize our main result here: All the liquid dependence in the
shear moduli comes into the wave dispersion formulas through
coefficient a (or equivalently  ).
Equations (59) and (60) show that
).
Equations (59) and (60) show that
| <I>aI> = 2<I>fI> - <I>cI> + <I>mI> + 3<I>GI><I>effI>. |
|
|
(67) |
For small fluctuations in 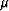 , coefficients a and c have comparable
magnitude dependence on the fluid effects, but of opposite sign. For large
fluctuations, the effects on a are much larger (quadratic) than
those on c (linear). Propagation at normal incidence will
never show much effect due to the liquids, while propagation at angles
closer to
, coefficients a and c have comparable
magnitude dependence on the fluid effects, but of opposite sign. For large
fluctuations, the effects on a are much larger (quadratic) than
those on c (linear). Propagation at normal incidence will
never show much effect due to the liquids, while propagation at angles
closer to 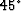 can show large enhancements in both quasi-P and quasi-SV
waves (when shear fluctuations are large), but still no effect on SH waves.
can show large enhancements in both quasi-P and quasi-SV
waves (when shear fluctuations are large), but still no effect on SH waves.





Next: COMPUTED EXAMPLES
Up: INTERPRETATION OF P AND
Previous: General analysis for VTI
Stanford Exploration Project
10/16/2003
![]() in
each layer should be replaced under undrained conditions by
in
each layer should be replaced under undrained conditions by
![]() .Making use of (56), we also have
.Making use of (56), we also have
![]() and the denominators
of (33), which have been approximated as
and the denominators
of (33), which have been approximated as
![]() instead of
instead of ![]() .Then, from (62), it is easy to see that
the final term in (34) vanishes to lowest
order, and that the remainder is given exactly by the shear modulus
fluctuation terms in brackets in (59) -- in complete agreement
with the final terms of (33). Then,
from (64), it follows that the leading
contribution to the factor
.Then, from (62), it is easy to see that
the final term in (34) vanishes to lowest
order, and that the remainder is given exactly by the shear modulus
fluctuation terms in brackets in (59) -- in complete agreement
with the final terms of (33). Then,
from (64), it follows that the leading
contribution to the factor ![]() is
is
![]() and
and ![]() for undrained porous media, and therefore more easily observed in
seismic, sonic, or ultrasonic data. When these effects are present,
the vertically polarized quasi-shear mode will show the highest
magnitude effect, the horizontally polarized shear mode will show
no effect, and the quasi-compressional mode will show an effect of
intermediate magnitude. It is known that these effects, when present,
are always strongest at
for undrained porous media, and therefore more easily observed in
seismic, sonic, or ultrasonic data. When these effects are present,
the vertically polarized quasi-shear mode will show the highest
magnitude effect, the horizontally polarized shear mode will show
no effect, and the quasi-compressional mode will show an effect of
intermediate magnitude. It is known that these effects, when present,
are always strongest at ![]() , and are diminished when the angle
of propagation is either
, and are diminished when the angle
of propagation is either ![]() or
or ![]() relative to the
layering direction. We will test these analytical predictions
with numerical examples in the next section.
relative to the
layering direction. We will test these analytical predictions
with numerical examples in the next section.
![]() ).
Equations (59) and (60) show that
).
Equations (59) and (60) show that