




Next: Analysis for layered media
Up: INTERPRETATION OF P AND
Previous: INTERPRETATION OF P AND
The correction terms for SV waves in weakly anisotropic media
are proportional to the factor
| 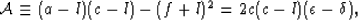 |
(47) |
which is sometimes called the anellipticity parameter. For the case
of weak anisotropy that we are considering here, the presence of this term
in (46) just introduces ellipticity into the move out, but the
higher order corrections that we neglected can introduce deviations
from ellipticity, hence anellipticity.
Clearly, from (46) for quasi-SV-waves [and in layered media
at this order of approximation], the anellipticity parameter
holds all the imformation about presence or absence of fluids that
is not already contained in the density factor 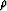 . So it will be
worth our time to study this factor in more detail. First note that,
after rearrangement, we have the general identity
. So it will be
worth our time to study this factor in more detail. First note that,
after rearrangement, we have the general identity
| 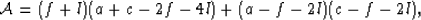 |
(48) |
which is true for all transversely isotropic media.
In some earlier work (Berryman, 2003), the author has shown that
it is convenient to introduce two special effective shear moduli
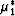 and
and 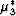 associated with a and c, namely,
associated with a and c, namely,
| 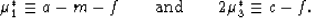 |
(49) |
Furthermore, it was shown that the combination defined by
| 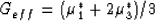 |
(50) |
plays a special role in the theory, as it is the only
effective shear modulus for the anisotropic
system that may also contain information about fluid content.
It turns out that (48) can be rewritten in terms of
this effective shear modulus if we first introduce two more parameters:
| ![\begin{eqnarray}
{\cal K} = f + l +
\left[{{1}\over{a-f-2l}}+{{1}\over{c-f-2l}}\right]^{-1}
\end{eqnarray}](img102.gif) |
(51) |
and
| ![\begin{eqnarray}
{\cal G} = \left[3G_{eff} + m - 4l\right]/3.
\end{eqnarray}](img103.gif) |
(52) |
Then, (48) can be simply rewritten as
| 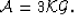 |
(53) |
This result is analogous to, but distinct from, a product formula
relating
the effective shear modulus Geff and the bulk modulus
| ![\begin{eqnarray}
K = f + \left[{{1}\over{a - m - f}} + {{1}\over{c -f}}\right]^{-1}
\end{eqnarray}](img105.gif) |
(54) |
to the eigenvalues of the elastic matrix according to
| 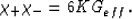 |
(55) |
In the isotropic limit for layered materials, when 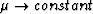 ,we have
,we have 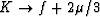 , while
, while 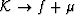 . So these two
parameters are not the same, but they do have strong similarities in
their behavior. In contrast,
. So these two
parameters are not the same, but they do have strong similarities in
their behavior. In contrast, 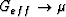 , while
, while
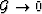 in the same limit. It is also possible to show
for layered materials that in general
in the same limit. It is also possible to show
for layered materials that in general 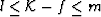 ,with the lower limit being optimum.
,with the lower limit being optimum.
Also, since Thomsen's 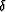 plays an important role in (45),
it is helpful to note that (25) can also be rewritten as
plays an important role in (45),
it is helpful to note that (25) can also be rewritten as
| ![\begin{eqnarray}
c\delta = -(c-f-2l)
\left[1 - {{c - f -2l}\over{2(c-l)}}\right],
\end{eqnarray}](img113.gif) |
(56) |
which shows that, at least for weakly anisotropic media,
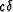 is very nearly a direct measure of the quantity c - f - 2l.
is very nearly a direct measure of the quantity c - f - 2l.





Next: Analysis for layered media
Up: INTERPRETATION OF P AND
Previous: INTERPRETATION OF P AND
Stanford Exploration Project
10/16/2003
![]() . So it will be
worth our time to study this factor in more detail. First note that,
after rearrangement, we have the general identity
. So it will be
worth our time to study this factor in more detail. First note that,
after rearrangement, we have the general identity
![]() and
and ![]() associated with a and c, namely,
associated with a and c, namely,
![]() plays an important role in (45),
it is helpful to note that (25) can also be rewritten as
plays an important role in (45),
it is helpful to note that (25) can also be rewritten as