




Next: INTERPRETATION OF P AND
Up: Berryman: Elastic and poroelastic
Previous: Approximate results for small
The general behavior of seismic waves in anisotropic media is well
known, and the equations are derived in many places including
Berryman (1979) and Thomsen (1986). The results are
| ![\begin{eqnarray}
\rho\omega_{\pm}^2 = {{1}\over{2}}
\left\{(a+l)k_1^2 + (c+l)k_3...
...\sqrt{[(a-l)k_1^2 - (c-l)k_3^2]^2 + 4(f+l)^2k_1^2k_3^2}\right\},
\end{eqnarray}](img77.gif) |
(35) |
for compressional (+) and vertically polarized shear (-) waves and
| 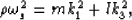 |
(36) |
for horizontally polarized shear waves, where 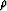 is the overall density,
is the overall density,
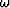 is the angular frequency, k1 and k3 are the horizontal
and vertical wavenumbers (respectively), and the velocities are given
simply by
is the angular frequency, k1 and k3 are the horizontal
and vertical wavenumbers (respectively), and the velocities are given
simply by 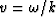 with
with 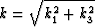 . The
SH wave depends only on elastic parameters
l and m, which are not dependent in any
way on layer
. The
SH wave depends only on elastic parameters
l and m, which are not dependent in any
way on layer 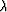 and therefore will play no role in the
poroelastic analysis. Thus, we can safely ignore SH except when
we want to check for shear wave splitting (bi-refringence) - in which
case the SH results will be useful for the comparisons.
and therefore will play no role in the
poroelastic analysis. Thus, we can safely ignore SH except when
we want to check for shear wave splitting (bi-refringence) - in which
case the SH results will be useful for the comparisons.
The dispersion relations for quasi-P- and quasi-SV-waves can be rewritten in a
number of instructive ways. One of these that we will choose for
reasons that will become apparent shortly is
| ![\begin{eqnarray}
\rho\omega_{\pm}^2 = {{1}\over{2}}
\left[(a+l)k_1^2 + (c+l)k_3^...
...(ak_1^2+ck_3^2)lk^2 +
\{(a-l)(c-l)-(f+l)^2\}k_1^2k_3^2]}\right].
\end{eqnarray}](img82.gif) |
|
| (37) |
Written this way, it is then obvious that the following two relations
hold:
| 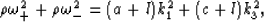 |
(38) |
and
| ![\begin{eqnarray}
\rho\omega_{+}^2\cdot\rho\omega_{-}^2 =
(ak_1^2+ck_3^2)lk^2 + [(a-l)(c-l)-(f+l)^2]k_1^2k_3^2,
\end{eqnarray}](img84.gif) |
(39) |
either of which could have been obtained directly from (35)
without the intermediate step of (37).
We are motivated to write the equations in this way in order to try to
avoid evaluating the square root in (35) directly. Rather,
we would like to arrive at a natural approximation that is quite
accurate, but does not involve the square root operation. From a
general understanding of the problem, it is clear that a reasonable
way of making use of (38) is to make the identifications
| 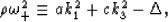 |
(40) |
and
| 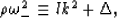 |
(41) |
with 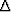 still to be determined. Then, substituting these
expressions into (39), we find that
still to be determined. Then, substituting these
expressions into (39), we find that
| ![\begin{eqnarray}
(ak_1^2 + ck_3^2 - lk^2 - \Delta)\Delta =
[(a-l)(c-l)-(f+l)^2]k_1^2k_3^2
\end{eqnarray}](img88.gif) |
(42) |
Solving (42) for 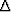 would just give the original
results back again. So the point of (42) is not to solve it
exactly, but rather to use it as the basis of an approximation scheme.
If
would just give the original
results back again. So the point of (42) is not to solve it
exactly, but rather to use it as the basis of an approximation scheme.
If 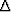 is small, then we can presumably neglect it inside the
parenthesis on the left hand side of (42),
or we could just keep a small number of terms in an expansion.
is small, then we can presumably neglect it inside the
parenthesis on the left hand side of (42),
or we could just keep a small number of terms in an expansion.
The leading term, and the only one we will consider here, is
| ![\begin{eqnarray}
\Delta = {{[(a-l)(c-l)-(f+l)^2]k_1^2k_3^2}\over
{(a-l)k_1^2 + (...
...simeq {{[(a-l)(c-l)-(f+l)^2]}\over
{(a-l)/k_3^2 + (c-l)/k_1^2}}.
\end{eqnarray}](img89.gif) |
(43) |
The numerator of this expression is known to be a positive quantity
for layered materials (Postma, 1955; Berryman, 1979). Furthermore, it
can be rewritten in terms of Thomsen's parameters as
| ![\begin{eqnarray}[(a-l)(c-l)-(f+l)^2]
= 2c(c-l)(\epsilon-\delta).
\end{eqnarray}](img90.gif) |
(44) |
Using the first of the identities noted earlier in (5),
we can also rewrite the first elasticity factor in the denominator as
![$a-l = (c-l)[1+2c\epsilon/(c-l)]$](img91.gif) . Combining these results in the
limit of
. Combining these results in the
limit of 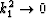 (for relatively small horizontal offset), we find that
(for relatively small horizontal offset), we find that
| 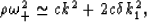 |
(45) |
and
| 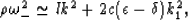 |
(46) |
with 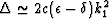 .Improved approximations to any desired order can be obtained with only
a little more effort by using (42) or (43)
instead of the first approximation used here. But (45) and
(46) are satisfactory for our present purposes.
.Improved approximations to any desired order can be obtained with only
a little more effort by using (42) or (43)
instead of the first approximation used here. But (45) and
(46) are satisfactory for our present purposes.





Next: INTERPRETATION OF P AND
Up: Berryman: Elastic and poroelastic
Previous: Approximate results for small
Stanford Exploration Project
10/16/2003
![\begin{eqnarray}
\rho\omega_{\pm}^2 = {{1}\over{2}}
\left[(a+l)k_1^2 + (c+l)k_3^...
...(ak_1^2+ck_3^2)lk^2 +
\{(a-l)(c-l)-(f+l)^2\}k_1^2k_3^2]}\right].
\end{eqnarray}](img82.gif)