Gradient

Optimization of the objective function in Equation (19) requires computation of its gradient with respect to slowness. The objective function J can be rewritten using the inner product as:

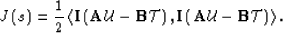$$J\left(s\right)= \frac{1}{2} \left< {\bf I}\left(\AA \u - {\... ...ght), {\bf I}\left(\AA \u - {\bf B}\mathcal T\right) \right\gt.$$ (20)

A perturbation of the function J is related to a perturbation of the wavefield by the relation:

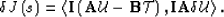$$\delta J\left(s\right)= \left< {\bf I}\left(\AA \u - {\bf B}\mathcal T\right), {\bf I}\AA \delta \u \right\gt.$$ (21)

If we replace 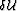$\delta \u$ from Equation (11) we obtain:

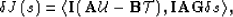$$\delta J\left(s\right)= \left< {\bf I}\left(\AA \u - {\bf B}\mathcal T\right), {\bf I}\AA {\bf G}\delta s \right\gt,$$ (22)

therefore the gradient of the objective function can be written as

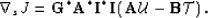$$\nabla_sJ= {\bf G}^* \AA^* {\bf I}^* {\bf I}\left(\AA \u - {\bf B}\mathcal T\right).$$ (23)

Following the definition of the operator 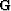${\bf G}$, we can write

$${\bf G}^* = {\bf S}^* {\bf E}^* \left[\left({\bf 1}- {\bf E}... ...bf E}^* \left[\left({\bf 1}- {\bf E}\right)^{ *} \right]^{-1} .$$ (24)

Finally, the expression for the gradient of the objective function with respect to slowness becomes  

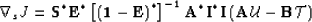$$\nabla_sJ= {\bf S}^* {\bf E}^* \left[\left({\bf 1}- {\bf E... ... \AA^* {\bf I}^* {\bf I}\left(\AA \u - {\bf B}\mathcal T\right)$$ (25)

which takes special forms depending on our choice of the operators 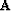$\AA$ and ${\bf B}$:

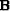WEMVA by TIF WEMVA by DSO

$$\nabla_sJ= {\bf S}^* {\bf E}^* \left[\left({\bf 1}- {\bf E}\right)^{ *} \right]^{-1} {\bf I}^* {\bf I}\left(\u - \mathcal T\right) \nabla_sJ= {\bf S}^* {\bf E}^* \left[\left({\bf 1}- {\bf E}\right)^{ *} \right]^{-1} {\bf D}^* {\bf I}^* {\bf I}{\bf D}\u$$

The gradient in Equation (25) is computed using the adjoint state method, which can be summarized by the following steps:

1.

Compute by downward continuation the wavefield

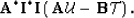$$\AA^* {\bf I}^* {\bf I}\left(\AA \u - {\bf B}\mathcal T\right).$$ (26)

2.

Compute by upward continuation the adjoint state wavefield

$$\mathcal W= \left[\left({\bf 1}- {\bf E}\right)^{ *} \right]... ...\AA^* {\bf I}^* {\bf I}\left(\AA \u - {\bf B}\mathcal T\right),$$ (27)

i.e. solve the adjoint state system

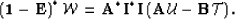$$\left({\bf 1}- {\bf E}\right)^{ *} \mathcal W= \AA^* {\bf I}^* {\bf I}\left(\AA \u - {\bf B}\mathcal T\right).$$ (28)

3.

Compute the gradient

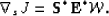$$\nabla_sJ= {\bf S}^* {\bf E}^* \mathcal W.$$ (29)