




Next: Example
Up: Theory of wave-equation MVA
Previous: Gradient
Minimizing the objective function J in Equation (19)
involves solving a non-linear least-squares problem
using the gradient given by Equation (25).
Alternatively, we can linearize the wavefield 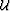 with respect to
a reference wavefield
with respect to
a reference wavefield 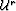
| 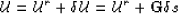 |
(30) |
and optimize
| 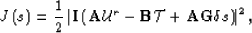 |
(31) |
which is a linear least-squares problem.
Equation (31) can also be represented by
fitting goals using the usual SEP terminology as:
| 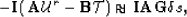 |
(32) |
which takes special forms depending on our choice of the
operators 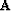 and
and 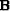 :
:
| WEMVA by TIF |
WEMVA by DSO |
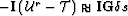 |
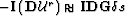 |
|---|





Next: Example
Up: Theory of wave-equation MVA
Previous: Gradient
Stanford Exploration Project
11/11/2002
![]() with respect to
a reference wavefield
with respect to
a reference wavefield ![]()