Next: Image transformation
Up: Theory of wave-equation MVA
Previous: Imaging by wavefield extrapolation
A perturbation of the wavefield at some depth level can
be derived from the background wavefield
by a simple application of the chain rule to
Equation (1):
| ![\begin{displaymath}
\delta \u_{z+\Delta z}= {\bf E}_z\left[\delta \u_{z } \right] + \delta {\bf E}_z \left[\u_{z } \right].\end{displaymath}](img18.gif) |
(5) |
This is also a recursive equation which can be written in
matrix form as
or in a more compact notation as:
| 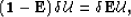 |
(6) |
where the operator 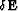 stands for a
perturbation of the extrapolation operator
stands for a
perturbation of the extrapolation operator 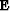 .
.
Biondi and Sava (1999) show that, at every depth
level, we can write the operator 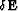 as a chain of
the extrapolation operator
as a chain of
the extrapolation operator 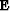 and a scattering operator
and a scattering operator  applied to the slowness perturbation
applied to the slowness perturbation 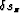 :
:
| ![\begin{displaymath}
\delta {\bf E}_z \left[\u_{z } \right] = {\bf E}_z\left[{\bf S}_z\left[\delta s_z \right] \right].\end{displaymath}](img24.gif) |
(7) |
The expression for the wavefield perturbation 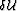 becomes
becomes
| ![\begin{displaymath}
\delta \u_{z+\Delta z}= {\bf E}_z\left[\delta \u_{z } \right] + {\bf E}_z\left[{\bf S}_z\left[\delta s_z \right] \right],\end{displaymath}](img26.gif) |
(8) |
which is also a recursive relation that can be written in matrix
form as
or in a more compact notation as:
| 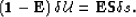 |
(9) |
The vector 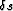 stands for the slowness perturbation.
stands for the slowness perturbation.
If we introduce the notation
| 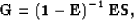 |
(10) |
we obtain a relation between a slowness perturbation
and the corresponding wavefield perturbation:
| 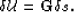 |
(11) |





Next: Image transformation
Up: Theory of wave-equation MVA
Previous: Imaging by wavefield extrapolation
Stanford Exploration Project
11/11/2002
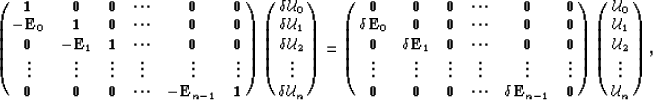
![]() as a chain of
the extrapolation operator
as a chain of
the extrapolation operator ![]() and a scattering operator
and a scattering operator ![]() applied to the slowness perturbation
applied to the slowness perturbation ![]() :
:
![]() becomes
becomes