




Next: Objective function
Up: Theory of wave-equation MVA
Previous: Wavefield perturbations
Migration velocity analysis is based on estimating the velocity
that optimizes certain properties of the migrated images.
In general, measuring such properties involves making
a transformation to the extrapolated wavefield by some function
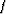 , followed by imaging:
, followed by imaging:
| ![\begin{displaymath}
\mathcal P_{z }= {\bf I}_z\left[\it{f}_z\left(\u_{z } \right) \right].\end{displaymath}](img33.gif) |
(12) |
In compact matrix form, we can write this relation as:
| 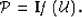 |
(13) |
The image 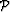 is subject to optimization from
which we derive the velocity updates.
is subject to optimization from
which we derive the velocity updates.
Examples of transformation functions are:
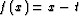 where t is a known target.
A WEMVA method based on this criterion optimizes
where t is a known target.
A WEMVA method based on this criterion optimizes
| ![\begin{displaymath}
\mathcal P_{z }:= {\bf I}_z\left[ \u_{z }- \mathcal T_{z } \right], \end{displaymath}](img37.gif) |
(14) |
where 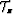 stands for the target wavefield.
For this method, we can use the acronym TIF
standing for target image fitting
Biondi and Sava (1999); Sava and Fomel (2002).
stands for the target wavefield.
For this method, we can use the acronym TIF
standing for target image fitting
Biondi and Sava (1999); Sava and Fomel (2002).
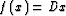 where D is a known operator.
A WEMVA method based on this criterion optimizes
where D is a known operator.
A WEMVA method based on this criterion optimizes
| ![\begin{displaymath}
\mathcal P_{z }:= {\bf I}_z\left[ {\bf D}_z\left[\u_{z } \right] \right]. \end{displaymath}](img40.gif) |
(15) |
If 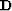 is a differential semblance operator,
we can use the acronym DSO standing for
differential semblance optimization
Stolk and Symes (2002); Symes and Carazzone (1991).
is a differential semblance operator,
we can use the acronym DSO standing for
differential semblance optimization
Stolk and Symes (2002); Symes and Carazzone (1991).
In general, both examples presented above belong to a
family of affine functions that can be written as
| ![\begin{displaymath}
\mathcal P_{z }:= {\bf I}_z\left[\AA_z\left[\u_{z } \right] - {\bf B}_z\left[\mathcal T_{z } \right] \right],\end{displaymath}](img42.gif) |
(16) |
or in compact matrix form as
| 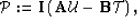 |
(17) |
where the operators 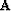 and
and 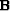 are known and
take special forms depending on the optimization criterion we
use. For example,
are known and
take special forms depending on the optimization criterion we
use. For example, 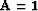 and
and 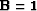 for TIF,
and
for TIF,
and 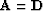 and
and 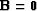 for DSO.
for DSO.
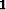 stands for the identity operator, and
stands for the identity operator, and
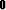 stands for the null operator.
stands for the null operator.





Next: Objective function
Up: Theory of wave-equation MVA
Previous: Wavefield perturbations
Stanford Exploration Project
11/11/2002