




Next: Wavefield perturbations
Up: Theory of wave-equation MVA
Previous: Theory of wave-equation MVA
Imaging by wavefield extrapolation (WE) is based on recursive
continuation of the wavefields 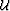 from a given depth level to the next
by means of an extrapolation operator
from a given depth level to the next
by means of an extrapolation operator 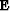 :
:
| ![\begin{displaymath}
\u_{z+\Delta z}= {\bf E}_z\left[\u_{z } \right]. \end{displaymath}](img6.gif) |
(1) |
This recursive relation can also be explicitly written in
matrix form as
or in a more compact notation as:
| 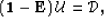 |
(2) |
where the vector 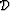 stands for the recorded data,
stands for the recorded data,
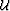 for the extrapolated wavefield,
for the extrapolated wavefield,
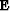 for the extrapolation operator and
for the extrapolation operator and
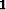 for the identity operator.
for the identity operator.
The wavefield at every depth level 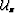 is imaged using an imaging operator
is imaged using an imaging operator 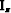 :
:
| ![\begin{displaymath}
\r_{z }= {\bf I}_z\left[\u_{z } \right],\end{displaymath}](img13.gif) |
(3) |
where 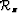 stands for the image at some depth level.
We can write the same relation in compact matrix form as:
stands for the image at some depth level.
We can write the same relation in compact matrix form as:
| 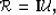 |
(4) |
where 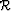 stands for the image, and
stands for the image, and
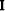 stands for the imaging operator which is
applied to the extrapolated wavefield
stands for the imaging operator which is
applied to the extrapolated wavefield 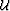 .
.





Next: Wavefield perturbations
Up: Theory of wave-equation MVA
Previous: Theory of wave-equation MVA
Stanford Exploration Project
11/11/2002
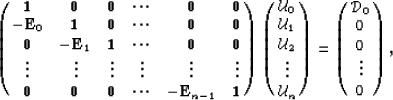
![]() is imaged using an imaging operator
is imaged using an imaging operator ![]() :
: