Reflector mapping imaging condition and image artifacts

Claerbout (1971) expresses the reflector mapping imaging condition as follows:  

$${\bf r}(x,z)=\frac{ {\bf u}(x,z,t_{d})}{ {\bf d}(x,z,t_{d})},$$ (1)

where x is the horizontal coordinate, z is the depth, and t_d is the time at which the source wavefield ${\bf d}(x,z,t_{d})$ and the receiver wavefield ${\bf u}(x,z,t_{d})$ coincide in time and space. This principle states that the reflectivity strength ${\bf r}(x,z)$ depends only on the source wavefield and on the receiver wavefield at time t_d.

A practical way to compute the reflectivity strength is discussed in Claerbout's paper Claerbout (1971). The reflectivity strength is computed as:  

$${\bf r}(x,z)= ({\bf u} \star {\bf d})(x,z,\tau =0),$$ (2)

where means cross-correlation and $\tau$ is the lag. This is commonly used in the industry. It has the advantage of being robust, but has the disadvantage of not computing the correct amplitudes Claerbout (1971).

A more general imaging condition can be stated, computing the reflectivity strength as:  

$${\bf r}(x,z)=\frac{ {\bf u}}{ {\bf d}}(x,z,\tau =0),$$ (3)

where the division means deconvolution in time of the receiver wavefield by the source wavefield for each (x,z) and $\tau$ is the lag. It has the potential of accounting for wavefield multipathing during imaging, thus avoiding the creation of image artifacts in the presence of velocity anomalies.

Figures  to show the comparison of wavefield deconvolution with wavefield cross-correlation imaging condition. The first row, in Figure , simulates the two wavefields coinciding at the reflector depth. The result of the cross-correlation and the result of the deconvolution is shown in the second row. For each case, the zero lag of the wavefield cross-correlation or the zero lag of the wavefield deconvolution is assigned as the reflectivity strength at this depth.

 

spike Figure 1 Wavefields coinciding at the reflector depth. (a) Source wavefield. (b) Receiver wavefield. (c) Wavefields cross-correlation. (d) Wavefields deconvolution.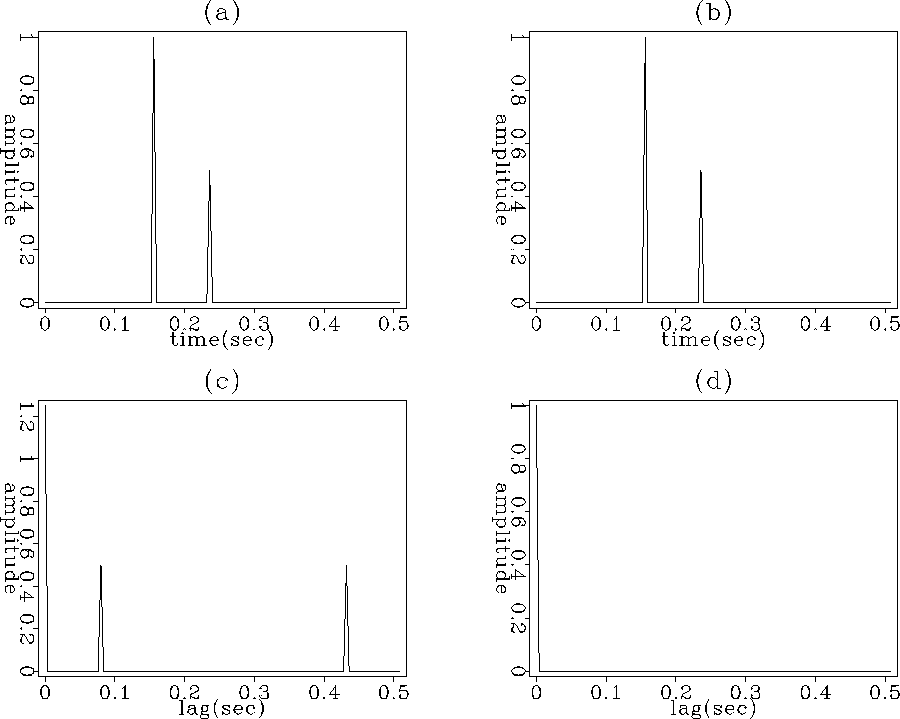

The first row in Figure  / simulates the two wavefields at a deeper / shallower depth than the reflector depth. The second row shows the result of the cross-correlation and the result of the deconvolution. The zero lag value of the wavefield cross-correlation has a value different than zero, thus creates an image artifact at a deeper / shallower depth. In the case of deconvolution imaging condition, the zero lag value is zero, thus no image artifacts are created.

 

spike1 Figure 2 Wavefields at a depth deeper the reflector depth. (a) Source wavefield. (b) Receiver wavefield. (c) Wavefields cross-correlation. (d) Wavefields deconvolution.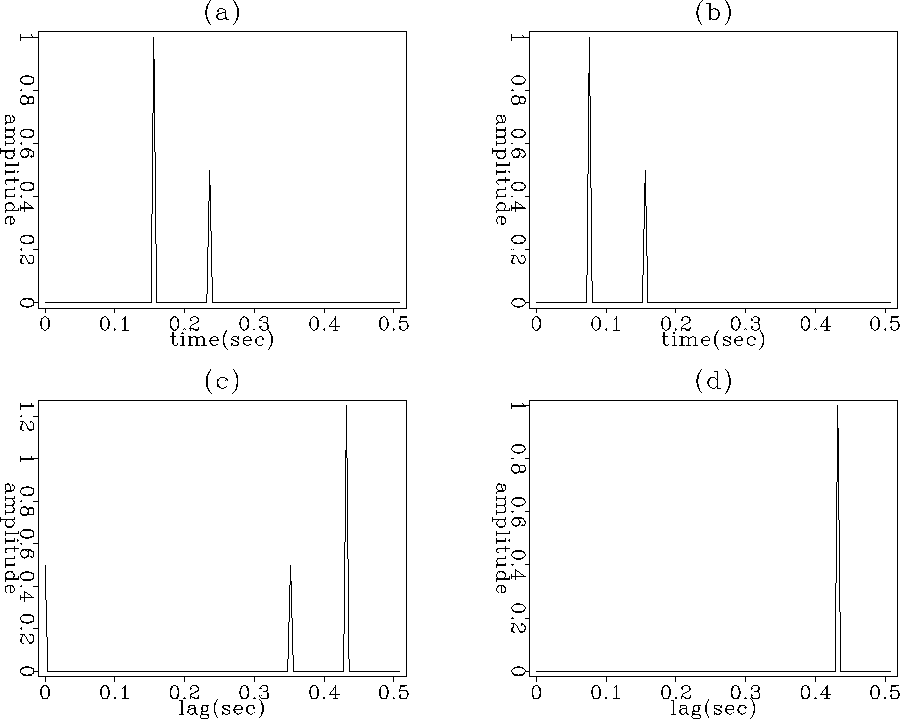

 

spike2 Figure 3 Wavefields at a depth shallower the reflector depth. (a) Source wavefield. (b) Receiver wavefield. (c) Wavefields cross-correlation. (d) Wavefields deconvolution.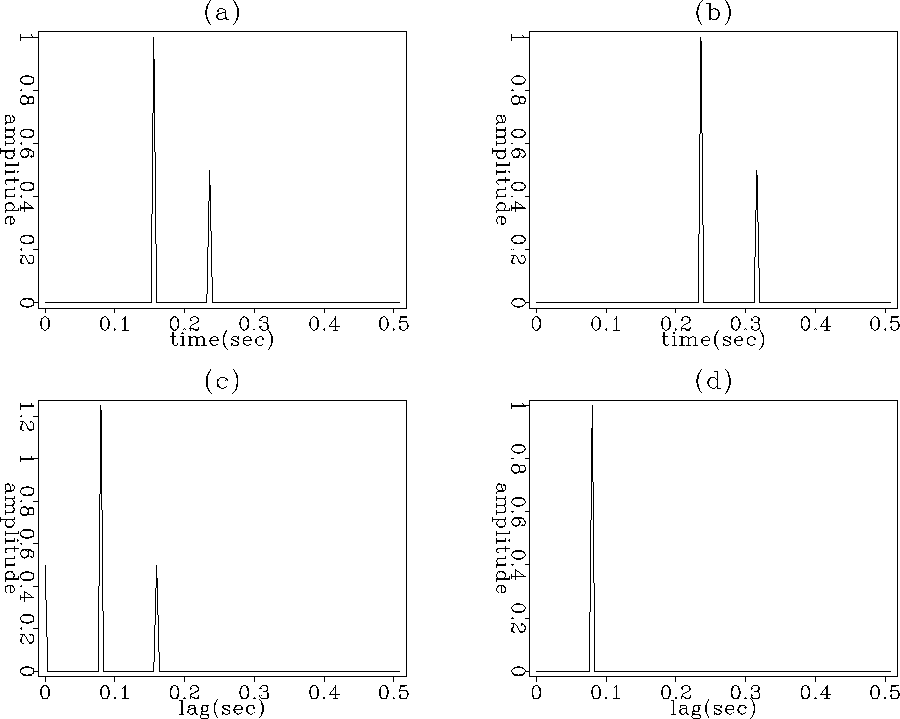

The imaging condition stated in equation (3) makes the strong assumption that the receiver wavefield ${\bf u}(x,z,t)$ can be computed by convolving the source wavefield ${\bf d}(x,z,t)$ by the reflectivity strength ${\bf r}(x,z)$. As we will discuss later, this is true at the reflector depth, but might not be true at a different depth.