




Next: Example
Up: Sava and Fomel: WEMVA
Previous: Higher accuracy linearizations
One can also consider the problem of estimating the slowness field
from wavefields using WEMVA in the general non-linear inversion
framework.
In particular, if 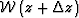 is the upgpoing wavefield at the bottom of a
layer and
is the upgpoing wavefield at the bottom of a
layer and 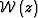 is the upgoing wavefield at the top of the layer,
the layer slowness s is constrained by the nonlinear equation
is the upgoing wavefield at the top of the layer,
the layer slowness s is constrained by the nonlinear equation
| ![\begin{displaymath}
F[s] = P[s]\,\mathcal W\left({z+\Delta z} \right)- \mathcal W\left({z } \right)= 0\;,\end{displaymath}](img44.gif) |
(18) |
where
![$P[s] = e^{i\,\k_z\left[s \right]}$](img45.gif) is the wave propagation operator.
is the wave propagation operator.
The Newton method applied to equation (18) amounts to
inversion of the linear system
| ![\begin{displaymath}
F'[s_k]\,(s_{k+1} - s_k) = - F[s_k]\;,\end{displaymath}](img46.gif) |
(19) |
where k is the nonlinear iteration counter (the iteration starts
with some a priori slowness model s0), and F'[s] is the Fréchet
derivative of the wave propagation operator. Since F[s] is
complex-valued, we can multiply both sides of system (19)
by the adjoint (complex-conjugate) operator F'[sk]T to obtain the
purely real system
| ![\begin{eqnarray}
F'[s_k]^T\,F'[s_k]\,(s_{k+1} - s_k)
& = & - F'[s_k]^T\,F[s_k]
...
...s_k)
& = & - \left(R'[s_k]^T\,R[s_k] + I'[s_k]^T\,I[s_k]\right)\;,\end{eqnarray}](img47.gif) |
(20) |
| |
where R[s] and I[s] are the real and imaginary parts of F[s].
Algorithm (21) is equivalent to the Gauss-Newton method
applied to the least-squares solution of
| ![\begin{eqnarray}
R[s] & \approx & 0\;, \\ I[s] & \approx & 0\;.\end{eqnarray}](img48.gif) |
(21) |
| (22) |
It is well-known
that the Newton and Newton-Gauss
methods possess fast convergence provided that the original estimate
s0 is sufficiently close to the solution. They may diverge
otherwise. To guarantee convergence, the norm (spectral radius)
of the Fréchet derivative G'[s] for the operator
| ![\begin{displaymath}
G[s] = s -
\frac
{ R'[s]^T\, R[s] + I'[s]^T\, I[s] }
{ R'[s]^T\,R'[s] + I'[s]^T\,I'[s] }\,\end{displaymath}](img49.gif) |
(23) |
must be strictly smaller than one in the vicinity of the solution that
contains the starting value s0. Convergence follows then from the
contraction mapping theorem. The speed of convergence is higher for
smaller norms.
It is important to realize that modifying the original nonlinear
Equation (18) may change the convergence behavior and lead
to faster convergence and wider convergence area. A particularly
meaningful way to modify Equation (18) is to multiply it by
![$P[s]^{-\xi}$](img50.gif) , where
, where 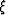 is a scalar between and 1. The
modified equation takes the form
is a scalar between and 1. The
modified equation takes the form
| ![\begin{displaymath}
F_\xi[s] = P[s]^{-\xi}\,F[s] = P[s]^{1-\xi}\,\mathcal W\left...
...lta z} \right)- P[s]^{-\xi}\,\mathcal W\left({z } \right)= 0\;.\end{displaymath}](img51.gif) |
(24) |
The case of 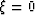 corresponds to the original system. Its
linearization with the Newton method leads to the Born approximation.
Analogously, the case of
corresponds to the original system. Its
linearization with the Newton method leads to the Born approximation.
Analogously, the case of 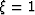 corresponds to the implicit method:
the two wavefields are compared at the bottom of the layer rather than
at the top. The case of
corresponds to the implicit method:
the two wavefields are compared at the bottom of the layer rather than
at the top. The case of 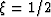 leads to the bilinear method: both
wavefields are continued to the middle of the layer for
comparison. Many other intermediate results are possible,
leads to the bilinear method: both
wavefields are continued to the middle of the layer for
comparison. Many other intermediate results are possible,





Next: Example
Up: Sava and Fomel: WEMVA
Previous: Higher accuracy linearizations
Stanford Exploration Project
6/7/2002
![]() is the upgpoing wavefield at the bottom of a
layer and
is the upgpoing wavefield at the bottom of a
layer and ![]() is the upgoing wavefield at the top of the layer,
the layer slowness s is constrained by the nonlinear equation
is the upgoing wavefield at the top of the layer,
the layer slowness s is constrained by the nonlinear equation
![]() , where
, where ![]() is a scalar between and 1. The
modified equation takes the form
is a scalar between and 1. The
modified equation takes the form