




Next: Newton's method and WEMVA
Up: Sava and Fomel: WEMVA
Previous: Born wave-equation MVA
As noted earlier, the approximation
| 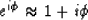 |
(9) |
corresponds to an
explicit numerical solution to the differential equation
(2). However, this is neither the only possible solution,
nor the most accurate, and furthermore it is only conditionally
stable.
We can, however, solve Equation (2) using other
numerical schemes. Two possibilities are
implicit numerical solutions, where we approximate
| 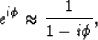 |
(10) |
or bilinear numerical solutions, where we approximate
| 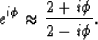 |
(11) |
Equations (9) and (10) are first order,
but Equation (11) is second order accurate as a function
of the phase 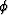 .Numerical schemes based on Equation (9) are
conditionally stable, but numerical schemes based on
Equations (10) and (11) are
unconditionally stable.
.Numerical schemes based on Equation (9) are
conditionally stable, but numerical schemes based on
Equations (10) and (11) are
unconditionally stable.
In the context of partial differential equations,
the bilinear approximation (11) is known under the name
of Crank-Nicolson and has been extensively used in migration by
downward-continuation using the paraxial wave equation
Claerbout (1985).
Figures 1 and 2 compare the
approximations in Equations (9), (10)
and (11) as a function of phase.
Both the explicit and implicit solutions lead to errors in
amplitude and phase, while the bilinear solution leads just
to errors in phase (Figure 2).
unit
Figure 1 Explicit, bilinear and implicit
approximations plotted on the unit circle. The solid line
corresponds to the exact exponential solution.
|
|  |

exap
Figure 2 Amplitude and phase errors for the
explicit, bilinear and implicit approximations.
|
|  |

If, for notation simplicity, we define
| 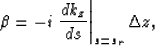 |
(12) |
the WEMVA equation (7) can be written as
| ![\begin{displaymath}
\Delta \mathcal W= \mathcal W_b\left[e^{\b \Delta s} -1 \right],\end{displaymath}](img29.gif) |
(13) |
and so the linearizations corresponding to the explicit, bilinear and
implicit solutions respectively become
| 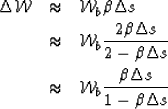 |
|
| |
| (14) |
Aparently, just the first equation in (14) provides
a linear relationship between 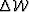 and
and 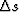 . However, a simple
re-arrangement of terms leads to
. However, a simple
re-arrangement of terms leads to
| ![\begin{eqnarray}
\Delta \mathcal W&\approx& \b \left[\mathcal W_b\right]\Delta s...
...&\approx& \b \left[\mathcal W_b+ \Delta \mathcal W\right]\Delta s.\end{eqnarray}](img31.gif) |
|
| |
| (15) |
For MVA, both the background (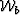 ) and perturbation wavefields (
) and perturbation wavefields (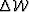 )
are known, so it is not a problem to incorporate them in the linear
operator. In any of the cases described in Equation (15),
the approximations can be symbolically written using the fitting goal
)
are known, so it is not a problem to incorporate them in the linear
operator. In any of the cases described in Equation (15),
the approximations can be symbolically written using the fitting goal
| 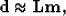 |
(16) |
where the data 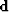 is the wavefield perturbation, and the
model
is the wavefield perturbation, and the
model 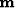 is the slowness perturbation. The same operator
is the slowness perturbation. The same operator 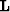 is used
for inversion in all situations, the only change being in the wavefield
that is fed into the linear operator. Therefore, the new
operators are not more expensive than the Born operator.
is used
for inversion in all situations, the only change being in the wavefield
that is fed into the linear operator. Therefore, the new
operators are not more expensive than the Born operator.
All linear relationships in Equation (15) belong to
a family of approximations of the general form
| ![\begin{eqnarray}
\Delta \mathcal W&\approx& \b \left[\mathcal W_b+ \xi \Delta \mathcal W\right]\Delta s.\end{eqnarray}](img37.gif) |
(17) |
The various approximations can be obtained using appropriate values for
the parameter 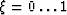 .All forms of Equation (17), however, are
approximations to the exact non-linear relation (13),
therefore they are all likely to break for large values of the phase, or
equivalently large values of the slowness perturbation or frequency.
Nevertheless, these approximations enable us to achieve higher accuray
in slowness estimation as compared to the simple Born approximation.
.All forms of Equation (17), however, are
approximations to the exact non-linear relation (13),
therefore they are all likely to break for large values of the phase, or
equivalently large values of the slowness perturbation or frequency.
Nevertheless, these approximations enable us to achieve higher accuray
in slowness estimation as compared to the simple Born approximation.
An interesting comparison can be made between the extreme members
of the sequence given by Equation (17):
for 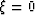 we use the background wavefield
we use the background wavefield 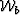 , and
for
, and
for 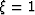 we use the full wavefield
we use the full wavefield 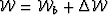 .
The physics of scattering would recommend that we use the later form,
since the scattered wavefield (
.
The physics of scattering would recommend that we use the later form,
since the scattered wavefield (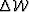 ) is generated by the total
wavefield (
) is generated by the total
wavefield (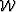 ), and not by an approximation of it (
), and not by an approximation of it (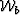 ), thus
naturally accounting for multiple scattering effects.
The later situation also corresponds to what is known in the
scattering literature as wavefield renormalization
Wang (1997). The details of these ideas and their implications
remain open for future research.
), thus
naturally accounting for multiple scattering effects.
The later situation also corresponds to what is known in the
scattering literature as wavefield renormalization
Wang (1997). The details of these ideas and their implications
remain open for future research.
Finally, we note that Equation (17) cannot be used for
forward modeling of the wavefield perturbations 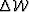 , except for the
particular case
, except for the
particular case 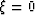 , since the output quantity is contained
in the operator itself. However, we can use this equation for inversion
for any choice of the parameter
, since the output quantity is contained
in the operator itself. However, we can use this equation for inversion
for any choice of the parameter 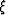 .
.





Next: Newton's method and WEMVA
Up: Sava and Fomel: WEMVA
Previous: Born wave-equation MVA
Stanford Exploration Project
6/7/2002


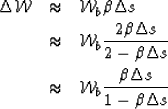
![\begin{eqnarray}
\Delta \mathcal W&\approx& \b \left[\mathcal W_b\right]\Delta s...
...&\approx& \b \left[\mathcal W_b+ \Delta \mathcal W\right]\Delta s.\end{eqnarray}](img31.gif)
![]() ) and perturbation wavefields (
) and perturbation wavefields (![]() )
are known, so it is not a problem to incorporate them in the linear
operator. In any of the cases described in Equation (15),
the approximations can be symbolically written using the fitting goal
)
are known, so it is not a problem to incorporate them in the linear
operator. In any of the cases described in Equation (15),
the approximations can be symbolically written using the fitting goal
![]() we use the background wavefield
we use the background wavefield ![]() , and
for
, and
for ![]() we use the full wavefield
we use the full wavefield ![]() .
The physics of scattering would recommend that we use the later form,
since the scattered wavefield (
.
The physics of scattering would recommend that we use the later form,
since the scattered wavefield (![]() ) is generated by the total
wavefield (
) is generated by the total
wavefield (![]() ), and not by an approximation of it (
), and not by an approximation of it (![]() ), thus
naturally accounting for multiple scattering effects.
The later situation also corresponds to what is known in the
scattering literature as wavefield renormalization
Wang (1997). The details of these ideas and their implications
remain open for future research.
), thus
naturally accounting for multiple scattering effects.
The later situation also corresponds to what is known in the
scattering literature as wavefield renormalization
Wang (1997). The details of these ideas and their implications
remain open for future research.
![]() , except for the
particular case
, except for the
particular case ![]() , since the output quantity is contained
in the operator itself. However, we can use this equation for inversion
for any choice of the parameter
, since the output quantity is contained
in the operator itself. However, we can use this equation for inversion
for any choice of the parameter ![]() .
.