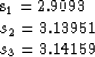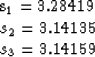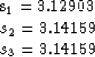Next: Physical interpretation
Up: Newton's method and WEMVA
Previous: Newton's method and WEMVA
The simplest case to study analytically is that of vertically-incident
waves in laterally homogeneous media. In this case, all operators
become functions of the scalar variable s (unknown layer
slowness). If, for a particular temporal frequency 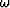 and the
layer thickness
and the
layer thickness 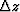 , we measure the slowness in units of
, we measure the slowness in units of
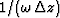 , the wave continuation operator is simply the
phase shift
, the wave continuation operator is simply the
phase shift
| 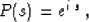 |
(25) |
and the fundamental nonlinear equation takes the form
| 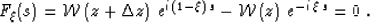 |
(26) |
Noting that
| 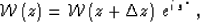 |
(27) |
where 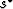 is the true slowness, and that the convergence of
Newton's method does not depend on scaling the equation by a constant,
we can modify equation (26) to the simpler form
is the true slowness, and that the convergence of
Newton's method does not depend on scaling the equation by a constant,
we can modify equation (26) to the simpler form
| 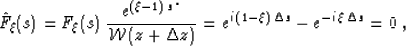 |
(28) |
where 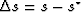 . The obvious solution of
Equation (28) is
. The obvious solution of
Equation (28) is 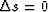 . Our task is to find the
convergence limits and their dependence on
. Our task is to find the
convergence limits and their dependence on 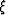 .
.
After a number of algebraic and trigonometric simplifications, the
operator G from equation (23) takes the form of the function
| 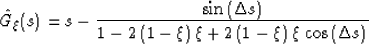 |
(29) |
Its derivative is
| ![\begin{displaymath}
\hat{G}_\xi'(s) = 2\,\sin^2 \left(\frac{\Delta s}{2}\right)\...
...i +
2\,(1 - \xi)\,\xi\,\cos \left(\Delta s\right)\right]^2}\;.\end{displaymath}](img64.gif) |
(30) |
The method will converge in the region around 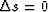 , where the
absolute value of
, where the
absolute value of 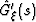 is strictly smaller than one. This
region (as a function of
is strictly smaller than one. This
region (as a function of 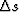 and
and 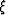 ) is plotted in
Figure 3. We can see that the convergence region has a
finite extent. Its width is the same for
) is plotted in
Figure 3. We can see that the convergence region has a
finite extent. Its width is the same for 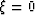 ,
, 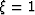 , and
, and
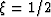 . Indeed,
. Indeed,
| 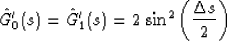 |
(31) |
and
| 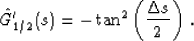 |
(32) |
In both cases, the absolute value of the derivative is smaller than
one if 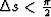 . If we take
. If we take 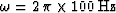 and
and 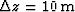 , then the convergence
radius is
, then the convergence
radius is 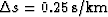 . At small
. At small 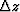 ,
,
| 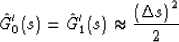 |
(33) |
and
| 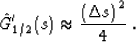 |
(34) |
The convergence rate is of the same order (cubic) but faster in the
case of the bilinear method (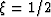 ), because of the twice smaller
constant. Here is an example of iterations starting with s0=2
and converging to
), because of the twice smaller
constant. Here is an example of iterations starting with s0=2
and converging to 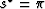 . The Born iteration:
The bilinear iteration:
A faster convergence can be achieved at some other values of
. The Born iteration:
The bilinear iteration:
A faster convergence can be achieved at some other values of 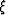 .Examining the Taylor series of
.Examining the Taylor series of 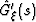 around
around 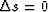 :
:
| ![\begin{displaymath}
\hat{G}_\xi'(s) \approx \left[1 - 6\,(1-\xi)\,\xi\right]\,
\frac{\left(\Delta s\right)^2}{2}\;,\end{displaymath}](img77.gif) |
(35) |
we find that the order of convergence is optimized for
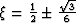 . In this case,
. In this case,
| ![\begin{displaymath}
\hat{G}_{1/2 \pm \sqrt{3}/6}'(s)
= \frac{4\,\sin^4{\left(\fr...
...right)}\right]^2}
\approx \frac{\left(\Delta s\right)^4}{36}\;,\end{displaymath}](img79.gif) |
(36) |
and the convergence is fifth order! The example
iterations with the optimal value of 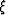 are:
The radius of convergence with the optimal value of
are:
The radius of convergence with the optimal value of 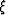 is
is
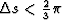 .
zo
.
zo
Figure 3 Convergence region for the Newton-Gauss method in the
vertical plane-wave example. Left: 3-D projection. Right: contours. The
non-white region on the right plot corresponds to the convergence
area. Horizontal axis: 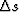 . Vertical axis:
. Vertical axis: 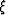 .
.

Of course, this analysis does not apply directly to the case of
non-vertical wave propagation and laterally inhomogenous slowness
fields. For reflection wavefields at multiple offsets, the symmetry
between downward and upward continuation is broken, as is clear from
the experimental results of this paper. However, the simple analysis
points to the potential benefits of modifying the Born approximation
in the wave-equation velocity estimation.





Next: Physical interpretation
Up: Newton's method and WEMVA
Previous: Newton's method and WEMVA
Stanford Exploration Project
6/7/2002