




Next: Higher accuracy linearizations
Up: Sava and Fomel: WEMVA
Previous: Downward-continuation migration
We define the wavefield perturbation 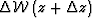 as
the difference between the wavefield propagated through the
medium with correct velocity
as
the difference between the wavefield propagated through the
medium with correct velocity 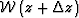 and the wavefield propagated
through the background medium
and the wavefield propagated
through the background medium 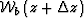 . With these definitions,
we can write
. With these definitions,
we can write
| 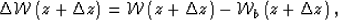 |
(6) |
or
| ![\begin{displaymath}
\Delta \mathcal W\left({z+\Delta z} \right)= \mathcal W_b \l...
... \k_z}
{d s} \right\vert _{s=s_r}\Delta s\Delta z} -1 \right].\end{displaymath}](img19.gif) |
(7) |
Equation (7) represents the
foundation of the wave-equation migration velocity analysis
method Biondi and Sava (1999). The major problem
with Equation (7) is that the wavefield 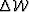 and
slowness perturbations
and
slowness perturbations 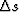 are not related through a linear relation,
therefore, for inversion purposes, we need to further approximate it
by linearizing the equation around the reference slowness (sr)
are not related through a linear relation,
therefore, for inversion purposes, we need to further approximate it
by linearizing the equation around the reference slowness (sr)
Biondi and Sava (1999) choose to linearize
Equation (7) using the Born
approximation (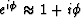 ),
from which the WEMVA equation becomes
),
from which the WEMVA equation becomes
| ![\begin{displaymath}
\Delta \mathcal W\left({z+\Delta z} \right)= \mathcal W_b \l...
...rac{d \k_z}
{d s} \right\vert _{s=s_r}\Delta s\Delta z\right].\end{displaymath}](img22.gif) |
(8) |
The problem with the Born linearization,
Equation (8), is that it is
is based on an assumption of small phase perturbation,
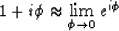
which mainly translates into small slowness perturbations. This fact
is more apparent if we recall that the linearization
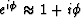 corresponds to an explicit
numerical solution of the differential equation (2),
a numerical solution which is notoriously unstable unless
precautions are taken to consider small propagation steps.
The main consequence of the limitations imposed by the
Born approximation is that WEMVA can only consider small
perturbations in the slowness model, which are likely too small
relative to the demands of real problems.
Since non-linear inversion is still not feasible for large size
problems like the ones typical for seismic imaging, we seek other
ways of linearizing Equation (7) which would
still enable us to solve our inversion problem within the framework
of linear optimization theory.
corresponds to an explicit
numerical solution of the differential equation (2),
a numerical solution which is notoriously unstable unless
precautions are taken to consider small propagation steps.
The main consequence of the limitations imposed by the
Born approximation is that WEMVA can only consider small
perturbations in the slowness model, which are likely too small
relative to the demands of real problems.
Since non-linear inversion is still not feasible for large size
problems like the ones typical for seismic imaging, we seek other
ways of linearizing Equation (7) which would
still enable us to solve our inversion problem within the framework
of linear optimization theory.





Next: Higher accuracy linearizations
Up: Sava and Fomel: WEMVA
Previous: Downward-continuation migration
Stanford Exploration Project
6/7/2002
![]() ),
from which the WEMVA equation becomes
),
from which the WEMVA equation becomes
![\begin{displaymath}
\Delta \mathcal W\left({z+\Delta z} \right)= \mathcal W_b \l...
...rac{d \k_z}
{d s} \right\vert _{s=s_r}\Delta s\Delta z\right].\end{displaymath}](img22.gif)
![]()