In the previous section we have seen that data gaps are a challenge for simple fold normalization. To fill the gaps, we want to use the information from traces recorded with geometry similar to the missing ones. The challenge is to devise a method that maximizes the image resolution and minimizes artifacts.
Given no a priori knowledge on the reflectors geometry, using the information from traces from the surrounding midpoints and same offset-azimuth range can cause a resolution loss because it may smooth true reflectivity changes. On the other hand, because of physical constraints on the reflection mechanism, the reflection amplitudes can be assumed to be a smooth function of the reflection angle and azimuth. This observation leads to the idea that smoothing the data over offset and azimuth could be performed without losing resolution. Ideally, such smoothing should be done over aperture angles (dip and azimuth) at the reflection location, not over offset and azimuth at the surface. However, smoothing at the reflectors would require a full migration of the data. The migration step would make the method dependent on the accurate knowledge of the interval velocity model. This reliance on the velocity model is inescapable when the imaging problems are caused by the complexities in velocity model itself, (e.g. subsalt illumination Prucha et al. (2001)), but it ought to be avoided when the imaging problems are caused by irregularities in the acquisition geometries.
In the context of least-squares inversion, smoothing along offset/azimuth in the model space (e.g. uniformly sampled offset/azimuth cubes) can be accomplished by introducing a model regularization term that penalizes variations of the seismic traces between the cubes. The simple least-squares problem of equation (8) then becomes
| |
||
![\begin{eqnarray}
{\bf D}_{{\bf h}}=
\frac{1}{1-\rho_D}
\left[ { \matrix{
1-\rho_...
... 0 & ... & \ddots &-\rho_D{\bf I} &{\bf I} \cr
} } \right].
\;\;\;\end{eqnarray}](img26.gif) |
(12) |
Regularization with a roughener operator such as ![]() has the computational drawback that it substantially worsens the conditioning
of the problem, making the solution more expensive.
However,
the problem is easy to precondition
because
has the computational drawback that it substantially worsens the conditioning
of the problem, making the solution more expensive.
However,
the problem is easy to precondition
because ![]() is easy to invert,
since it is already factored in a lower
block-diagonal operator
is easy to invert,
since it is already factored in a lower
block-diagonal operator
![]() and in an upper block-diagonal operator
and in an upper block-diagonal operator
![]() ,that can be inverted by recursion.
Therefore, we can write the preconditioned
least-squares problem
,that can be inverted by recursion.
Therefore, we can write the preconditioned
least-squares problem
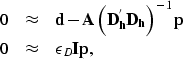 |
||
To take into account fold variations we can introduce a diagonal scaling factor, by applying the same theory discussed in the previous section. The weights for the regularized and preconditioned problem are thus computed as
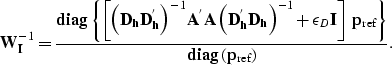 |
(13) |
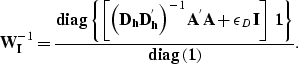 |
(14) |
The solution of the problem obtained by normalizing the preconditioned adjoint is
| |
(15) |
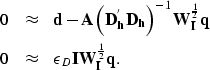 |
||