Stacking is the operation of averaging seismic traces by summation. It is an effective way to reduce the size of data sets and to enhance reflections while attenuating noise. To avoid attenuating the signal together with the noise, the reflections need to be coherent among the traces that are being stacked. A common method to increase trace coherency is to apply Normal Moveout (NMO). NMO is a first-order correction for the differences in timings among the reflections in traces recorded at different offsets. Global stacking of all the traces recorded at the same midpoint location, no matter their offset and azimuth, is the most common type of stacking. Partial stacking averages only those traces with offset and azimuth within a given range.
The first problem that we encounter
when stacking 3-D prestack data
is that,
because of acquisition geometry irregularities,
data traces do not share the same exact midpoint location.
Stacking 3-D prestack data
is thus the combination of two processes:
spatial interpolation followed by averaging.
To start our analysis
we define a simple linear model
that links the recorded traces (at arbitrary midpoint locations)
to the stacked volume (defined on a regular grid).
Each data trace is the result of interpolating the stacked traces,
and it is equal to the weighted sum
of the neighboring stacked traces.
The interpolation weights
are functions of the distance between the midpoint location of
the model trace and the midpoint location of the data trace.
The sum of all the weights corresponding to one
data trace is usually equal to one.
Because the weights are independent from time along
the seismic traces, for sake of notation simplicity,
we collapse the time axis
and consider each element di of the data space (recorded data)
![]() , and each element mj of the model space
, and each element mj of the model space ![]() (stacked volume),
as representing a whole trace.
The relationship between data and model is linear and
can be expressed as,
(stacked volume),
as representing a whole trace.
The relationship between data and model is linear and
can be expressed as,
| |
(1) |
| |
(2) |
![\begin{eqnarray}
{\bf m}=
\left[ { \matrix{
{\bf m}_{{\bf h}_1} \cr
\vdots \cr
{...
...m}_{{\bf h}_i} \cr
\vdots \cr
{\bf m}_{{\bf h}_n} \cr
} } \right].\end{eqnarray}](img6.gif) |
(3) |
Stacking is the summing of the data traces into the model traces
weighted by the interpolation weights.
In operator notation, stacking can be represented as
the application of the adjoint operator ![]() to the data traces Claerbout (1998);
that is,
to the data traces Claerbout (1998);
that is,
| (4) |
| |
(5) |
| |
(6) |
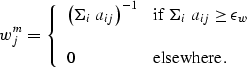 |
(7) |
We derived the fold normalization by a simple heuristic, and it may seem an ad hoc solution to the problem of normalizing the output of stacking. However, it can be shown that the weights used by fold normalization can be derived from applying the general theory of inverse least-squares to the stacking normalization problem Biondi (1999). The least-squares problem is
| |
(8) |
| |
(9) |
where the operator ![]() is often referred as the pseudoinverse
Strang (1986).
is often referred as the pseudoinverse
Strang (1986).
Applying the least-squares inverse is equivalent
to applying the adjoint operator ![]() followed by a spatial filtering of the model
space given by the inverse of
followed by a spatial filtering of the model
space given by the inverse of ![]() .The fold normalization can be seen as a particular
approximation of the inverse of
.The fold normalization can be seen as a particular
approximation of the inverse of ![]() with
a diagonal operator.
Because of the size of the problem,
computing the exact inverse of
with
a diagonal operator.
Because of the size of the problem,
computing the exact inverse of ![]() is not straightforward.
We have thus two choices:
1) to compute an analytical approximation to the inverse;
2) to use an iterative method to compute a
numerical approximation to the inverse.
Even if we follow the second strategy,
the availability of an analytical approximation to the inverse
is useful, because the approximate inverse can be used
as a preconditioner to accelerate the convergence
of the iterative inversion.
is not straightforward.
We have thus two choices:
1) to compute an analytical approximation to the inverse;
2) to use an iterative method to compute a
numerical approximation to the inverse.
Even if we follow the second strategy,
the availability of an analytical approximation to the inverse
is useful, because the approximate inverse can be used
as a preconditioner to accelerate the convergence
of the iterative inversion.
We will discuss two methods for approximating the inverse
of ![]() .The first method is algebraic and it is based on the direct manipulation
of the elements of
.The first method is algebraic and it is based on the direct manipulation
of the elements of ![]() ,such as extracting its diagonal or summing the elements
in its columns (or rows).
The second method is based on the idea that for capturing the most
significant properties of
,such as extracting its diagonal or summing the elements
in its columns (or rows).
The second method is based on the idea that for capturing the most
significant properties of ![]() by measuring its effects when applied to a reference model (
by measuring its effects when applied to a reference model (![]() )Claerbout and Nichols (1994); Rickett (2001).
)Claerbout and Nichols (1994); Rickett (2001).
Although these two methods seems unrelated,
they yield equivalent results for specific choices
of ![]() .Therefore, the second method can be used to analyze
the assumptions that underly the possible choices
of approximations.
.Therefore, the second method can be used to analyze
the assumptions that underly the possible choices
of approximations.