




Next: Imaging of a 3-D
Up: Model regularization and preconditioning
Previous: Model regularization and preconditioning
The main drawback of the method described above is
that smoothing over offset/azimuth cubes
by the inverse of the simple roughener operator
expressed in equation (13)
may result in loss of resolution when
geological dips are present.
It is well know that
dipping events are not flattened
by NMO with the same velocity as flat events.
However, the method is easily generalized by substitution
of the identity matrix in the lower diagonal of 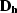 with an appropriate operator that correctly
transforms a common offset-azimuth cube
into an equivalent cube with a different offset and azimuth.
This can be accomplished by AMO Biondi et al. (1998).
Since the cubes to be transformed are uniformly sampled
we can use a Fourier-domain formulation
of AMO that is both efficient and straightforward to
implement Vlad and Biondi (2001).
The roughener operator that includes AMO
is then expressed as
with an appropriate operator that correctly
transforms a common offset-azimuth cube
into an equivalent cube with a different offset and azimuth.
This can be accomplished by AMO Biondi et al. (1998).
Since the cubes to be transformed are uniformly sampled
we can use a Fourier-domain formulation
of AMO that is both efficient and straightforward to
implement Vlad and Biondi (2001).
The roughener operator that includes AMO
is then expressed as
| ![\begin{eqnarray}
\widetilde{\bf D}_{{\bf h}}=
\frac{1}{1-\rho_D}
\left[ { \matri...
...&\ddots&-\rho_D{\bf T}_{{\bf h}_{n-1,n}} &{\bf I} \cr
} } \right],\end{eqnarray}](img40.gif) |
(16) |
where
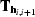 is the AMO operator that transforms the offset-azimuth cube i
into the offset-azimuth cube i+1.
The
is the AMO operator that transforms the offset-azimuth cube i
into the offset-azimuth cube i+1.
The 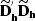 operator can also be easily inverted
by recursion and thus the least-squares problem
obtained by substituting
operator can also be easily inverted
by recursion and thus the least-squares problem
obtained by substituting
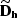 for
for 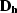 in
equations (12) can also be easily
preconditioned and normalized using the same
techniques described in
equations (14-18).
in
equations (12) can also be easily
preconditioned and normalized using the same
techniques described in
equations (14-18).





Next: Imaging of a 3-D
Up: Model regularization and preconditioning
Previous: Model regularization and preconditioning
Stanford Exploration Project
9/18/2001
![\begin{eqnarray}
\widetilde{\bf D}_{{\bf h}}=
\frac{1}{1-\rho_D}
\left[ { \matri...
...&\ddots&-\rho_D{\bf T}_{{\bf h}_{n-1,n}} &{\bf I} \cr
} } \right],\end{eqnarray}](img40.gif)
![\begin{eqnarray}
\widetilde{\bf D}_{{\bf h}}=
\frac{1}{1-\rho_D}
\left[ { \matri...
...&\ddots&-\rho_D{\bf T}_{{\bf h}_{n-1,n}} &{\bf I} \cr
} } \right],\end{eqnarray}](img40.gif)