




Next: Conclusions
Up: Compensating for irregular shot
Previous: Shot illumination examples
The analysis above ignores the v(z) true-amplitude
WKBJ Green's functions Stolt and Benson (1986) discussed in
section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
It also ignores the effect the imaging condition has on dipping
events. Sava et al. (2001) discuss this in more detail; but
the Jacobian associated with the transformation from temporal
frequency to vertical wavenumber causes the slight attenuation of
dipping events visible in Figure
.
It also ignores the effect the imaging condition has on dipping
events. Sava et al. (2001) discuss this in more detail; but
the Jacobian associated with the transformation from temporal
frequency to vertical wavenumber causes the slight attenuation of
dipping events visible in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
Both of these effects, however, are well-understood, and they
can be compensated for in a true-amplitude migration operator,
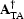 .
Such a true-amplitude migration operator will no longer be the true
adjoint of the forward modeling operator;
but we can still build and solve the system of normal equations,
.
Such a true-amplitude migration operator will no longer be the true
adjoint of the forward modeling operator;
but we can still build and solve the system of normal equations,
| 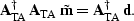 |
(89) |
Since 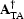 replaces
replaces 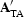 , the
solution to this system will not be equivalent to the solution
that minimizes the residual error in fitting goal,
, the
solution to this system will not be equivalent to the solution
that minimizes the residual error in fitting goal,
| 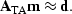 |
(90) |
However, if a pair of invertible operators (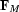 and
and 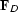 ) exist, such that
) exist, such that
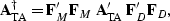
then the solution to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be the same as
the solution that minimizes the residual error in fitting goal,
) will be the same as
the solution that minimizes the residual error in fitting goal,
| 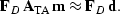 |
(91) |
The solution will also converge faster under an iterative inversion
scheme since
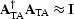 .
.





Next: Conclusions
Up: Compensating for irregular shot
Previous: Shot illumination examples
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
It also ignores the effect the imaging condition has on dipping
events. Sava et al. (2001) discuss this in more detail; but
the Jacobian associated with the transformation from temporal
frequency to vertical wavenumber causes the slight attenuation of
dipping events visible in Figure
.
It also ignores the effect the imaging condition has on dipping
events. Sava et al. (2001) discuss this in more detail; but
the Jacobian associated with the transformation from temporal
frequency to vertical wavenumber causes the slight attenuation of
dipping events visible in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![]() .
Such a true-amplitude migration operator will no longer be the true
adjoint of the forward modeling operator;
but we can still build and solve the system of normal equations,
.
Such a true-amplitude migration operator will no longer be the true
adjoint of the forward modeling operator;
but we can still build and solve the system of normal equations,
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) will be the same as
the solution that minimizes the residual error in fitting goal,
) will be the same as
the solution that minimizes the residual error in fitting goal,