For a generic forward modeling operator, ![]() , and more data
values than unknown model parameters, the model estimate,
, and more data
values than unknown model parameters, the model estimate,
![]() that best predicts the data in a least-squares sense
is given by the solution to the normal equations,
that best predicts the data in a least-squares sense
is given by the solution to the normal equations,
| |
(82) |
Often for large geophysical problems such as migration, this system of equations is not solved directly, rather the solution is estimated by an iterative method such as conjugate gradients [e.g. Nemeth et al. (1999); Prucha et al. (2000)].
Obviously, however, if the operator, ![]() is
diagonal, it is easy to calculate
is
diagonal, it is easy to calculate ![]() , and
obtain the L2 solution directly from the adjoint (migrated) image.
Rather than iterate with the entire migration operator, in this
section I will consider the effect of explicitly inverting the chain
of operators that make up wave-equation modeling, looking for
situations in which
, and
obtain the L2 solution directly from the adjoint (migrated) image.
Rather than iterate with the entire migration operator, in this
section I will consider the effect of explicitly inverting the chain
of operators that make up wave-equation modeling, looking for
situations in which ![]() is diagonal.
is diagonal.
The shot-profile modeling operator, given in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), can also be expressed in terms of the
extrapolation operator,
), can also be expressed in terms of the
extrapolation operator, ![]() , as
, as
| (83) | ||
| (84) |
The classical L2 estimate of ![]() is given by
is given by
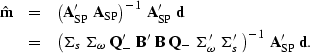 |
(85) | |
| (86) |
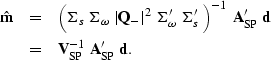 |
(87) | |
| (88) |
This weighting function is also equivalent to the upgoing/downgoing
wavefield imaging condition originally proposed by
Claerbout (1971).
Field data results Jacobs (1982) show
this imaging condition is very susceptible to noise.
However, dividing by the downgoing wavefield after migration, rather
than directly as part of the imaging condition, has a significant
advantage: the choice of appropriate local smoothing and
stabilization parameters (e.g. ![]() ) may be made after the
migration is finished.
) may be made after the
migration is finished.
Duquet et al. (2000) calculate the subsurface illumination for
Kirchhoff migration by summing all contributions from a single
scatterer that get modeling into dataspace. The shot illumination
described here is a special case of Duquet's illumination that assumes
all scattered energy is recorded.
However, the extra cost of calculating shot illumination is negligible
compared to the cost of a single migration, and Duquet's approach to
calculating illumination is not appropriate for wave-equation
migration schemes (see Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).