Migration is the process of downward continuation of the
wavefield plus the application of the imaging condition (t=0). The downward
continuation process can be achieved in the Fourier domain
Gazdag (1978); Stolt (1978). The phase-shift method extrapolates
the wavefield downwards with ![]() , where
the dispersion relation of the
scalar wave equation defines kz Claerbout (1985):
, where
the dispersion relation of the
scalar wave equation defines kz Claerbout (1985):
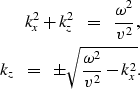 |
||
| (1) |
The use of (1) for calculating kz obscures two
aspects of it: first, which of the two square roots is
intended, and second, what happens when
![]() (evanescent waves).
Claerbout (1999a) emphasizes the fact that for coding and
theoretical work it is necessary to define kz for both
positive and negative
(evanescent waves).
Claerbout (1999a) emphasizes the fact that for coding and
theoretical work it is necessary to define kz for both
positive and negative ![]() , and for all kx values.
, and for all kx values.
The inclusion of the damping factor can solve the ambiguity
in the kz selection. This damping is traditionally included
as a cutoff frequency; Claerbout (1999a) defines a function ![]() that includes this cutoff frequency as:
that includes this cutoff frequency as:
| |
(2) |
This function (2) has a positive real part (Figure 1),
which implies that we can extrapolate waves safely with ![]() .
However, since the damping factor has been included as a cutoff frequency
we can lose frequency information with an inappropriate choice of
.
However, since the damping factor has been included as a cutoff frequency
we can lose frequency information with an inappropriate choice of
![]() .
.
|
fradan
Figure 1 Function (2) for an |  |
A theoretical redefinition of R=ikz that incorporates causality and viscosity concepts will not only solve for the ambiguity of the kz selection but also preserve the frequency content of our original data.