The principle of causality: no response before a stimulus, is not considered
in the R definition [equation (2)]. The omission of causality
translates into improper behavior of the high frequencies.
In order to include causality into the definition of R, let ![]() be the causal,
positive, discrete representation of the differentiation operator,
be the causal,
positive, discrete representation of the differentiation operator,
| (3) |
which is simplified by writting ![]() .
.
Claerbout (1985) proposes the use of the following Muir recursion starting from R0=s:
| |
(4) |
This recursion produces a continuous fraction. Studying the limit for ![]() we obtain:
we obtain:
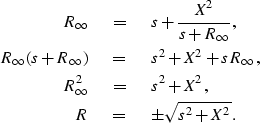 |
||
| (5) |
If we let X2 = v2 kx2 in equation (5) then R is ![]() .
The retarded time expression of
.
The retarded time expression of ![]() [equation (6)] will
downward continue, in time, the data for phase-shift migration.
[equation (6)] will
downward continue, in time, the data for phase-shift migration.
| |
(6) |
The following change of variables:
| (7) |
transforms the Muir recursion (4) into:
| |
(8) |
Again, taking the limit for ![]() in this recursion we will obtain
in this recursion we will obtain
| (9) |
This quadratic expression yields to two square roots for ![]() ,
,
| (10) |
We need to select the one that is able to handle the evanescent region, i.e, the square root that goes to zero at kx = 0, which corresponds to the positive square root.
| |
(11) |
| |
(12) |
I already showed that the real part of ![]() is positive
(Figure 1); therefore,
is positive
(Figure 1); therefore, ![]() , as defined in
equation (12), also has a positive real part.
, as defined in
equation (12), also has a positive real part.
Finally, we downward continue the data in the Fourier domain by multiplying by:
| |
(13) |
Expression (13) incorporates the causality and viscosity concepts in phase shift migration, controls the evanescent energy and will not allow discontinuity between evanescent and non-evanescent regions.