




Next: Approximating the signal PEF
Up: Theory review
Previous: Wiener-like method
In contrast to the Wiener-like method which filters the noise, the
following method aims to model the noise and then subtract it from
the input data. In this section, we show that the formalism used
by Nemeth (1996) can help to better separate correlated noise and signal.
But first, we detail the similarities and differences between
the Wiener-like and the subtraction method.
In equation (2), the noise and signal PEFs filter
the data components. Alternatively, building on Nemeth (1996), the noise
and signal nonstationary PEF can predict the data components via a
deconvolution as follows:
| 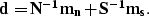 |
(4) |
We call 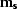 the signal model component and
the signal model component and 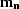 the noise model
component (not to be confused with the noise model that we use to compute the
noise PEF). Clearly,
the noise model
component (not to be confused with the noise model that we use to compute the
noise PEF). Clearly, 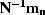 models the noise vector n
and
models the noise vector n
and 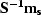 the signal vector s.
Because we use PEFs in equation (4), this approach is
pattern-based in essence.
With
the signal vector s.
Because we use PEFs in equation (4), this approach is
pattern-based in essence.
With 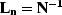 and
and 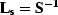 ,using linear algebra, we can prove that the least-squares
solution of
,using linear algebra, we can prove that the least-squares
solution of 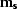 and
and 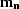 is
is
| 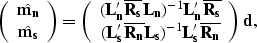 |
(5) |
with
| 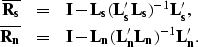 |
|
| (6) |
The operators 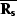 and
and 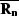 can be
seen as signal and noise filters respectively since
can be
seen as signal and noise filters respectively since
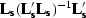 and
and
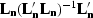 are the data resolution operators for
the signal and the noise, respectively. In the appendix B, we give a geometrical
interpretation for both
are the data resolution operators for
the signal and the noise, respectively. In the appendix B, we give a geometrical
interpretation for both 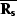 and
and 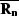 .
.
The degree of orthogonality between the noise operator 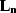 and
the signal operator
and
the signal operator 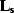 restricts the existence of
restricts the existence of
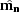 and
and 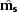 in equation (5). If the two
operators overlap completely, the Hessians
in equation (5). If the two
operators overlap completely, the Hessians 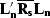 and
and 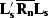 are not
invertible. If the two operators overlap only partially,
Nemeth (1996) proves that the separability of the signal
and noise can be improved if we introduce a regularization term.
If we use a model space regularization Fomel (1997),
we have
are not
invertible. If the two operators overlap only partially,
Nemeth (1996) proves that the separability of the signal
and noise can be improved if we introduce a regularization term.
If we use a model space regularization Fomel (1997),
we have
| 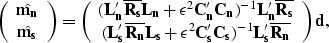 |
(7) |
with 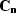 and
and 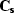 the regularization operators
for the noise model
the regularization operators
for the noise model 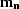 and the signal model
and the signal model 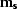 .A data space regularization can also improve the separation but
will not be considered here.
.A data space regularization can also improve the separation but
will not be considered here.
In equation (4),
the outcome of the inversion is 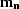 and
and 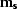 .
The estimated signal
.
The estimated signal  is then easily derived as follows:
is then easily derived as follows:
| 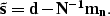 |
(8) |
We call this new method the subtraction method. In the next two sections,
we compare the Wiener-like approach and the subtraction
method for ground-roll and multiple attenuation.





Next: Approximating the signal PEF
Up: Theory review
Previous: Wiener-like method
Stanford Exploration Project
4/29/2001
![]() and
the signal operator
and
the signal operator ![]() restricts the existence of
restricts the existence of
![]() and
and ![]() in equation (5). If the two
operators overlap completely, the Hessians
in equation (5). If the two
operators overlap completely, the Hessians ![]() and
and ![]() are not
invertible. If the two operators overlap only partially,
Nemeth (1996) proves that the separability of the signal
and noise can be improved if we introduce a regularization term.
If we use a model space regularization Fomel (1997),
we have
are not
invertible. If the two operators overlap only partially,
Nemeth (1996) proves that the separability of the signal
and noise can be improved if we introduce a regularization term.
If we use a model space regularization Fomel (1997),
we have
![]() and
and ![]() .
The estimated signal
.
The estimated signal ![]() is then easily derived as follows:
is then easily derived as follows: