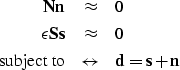Next: Subtraction method
Up: Theory review
Previous: Theory review
A constrained least-squares problem using PEFs gives a similar
expression for the noise estimation to the Wiener method.
To see this, consider the recorded data to be the simple superposition
of signal and noise, that is 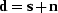 .For the special case of uncorrelated signal and noise,
the so-called Wiener estimator, is a filter which when applied
to the data, yields an optimal (in a least-squares sense)
estimate of the embedded signal Castleman (1996).
The frequency response of this filter is
.For the special case of uncorrelated signal and noise,
the so-called Wiener estimator, is a filter which when applied
to the data, yields an optimal (in a least-squares sense)
estimate of the embedded signal Castleman (1996).
The frequency response of this filter is
| 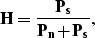 |
(1) |
where 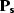 and
and 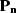 are the signal and noise power
spectra, respectively.
are the signal and noise power
spectra, respectively.
Similarly, Abma (1995) solved a
constrained least squares problem to separate signal from
spatially uncorrelated noise:
| 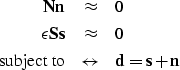 |
|
| (2) |
| |
where the operators 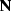 and
and 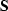 represent
t-x domain convolution with nonstationary
PEF which whiten the unknown noise
represent
t-x domain convolution with nonstationary
PEF which whiten the unknown noise  and signal
and signal  ,
respectively, and
,
respectively, and  is a Lagrange multiplier. Minimizing the quadratic
objective function suggested by equation (2) with respect
to
is a Lagrange multiplier. Minimizing the quadratic
objective function suggested by equation (2) with respect
to  leads to the following expression for the estimated signal:
By construction, the frequency response of a PEF approximates
the inverse power spectrum of the data from which it was estimated.
Thus we see that the approach of equation (2)
is similar to the Wiener reconstruction process. We refer to
this approach as a ``Wiener-like'' method. It has been
successfully used by Brown and Clapp (2000) for ground-roll attenuation
and by Clapp and Brown (2000) for multiple separation.
leads to the following expression for the estimated signal:
By construction, the frequency response of a PEF approximates
the inverse power spectrum of the data from which it was estimated.
Thus we see that the approach of equation (2)
is similar to the Wiener reconstruction process. We refer to
this approach as a ``Wiener-like'' method. It has been
successfully used by Brown and Clapp (2000) for ground-roll attenuation
and by Clapp and Brown (2000) for multiple separation.





Next: Subtraction method
Up: Theory review
Previous: Theory review
Stanford Exploration Project
4/29/2001