




Next: Subtracting the coherent noise
Up: Subtracting coherent noise
Previous: Subtracting coherent noise
For this first series of tests, I used the synthetic data in Figure
1. The first stage, after which I
estimate a PEF from the residual, took 45 iterations. The filter
is one-dimensional with 30 coefficients (a=30,1).
In the second stage, I use the inverse of the filter as the
noise modeling operator shown in equation (4).
The subtraction results in a reduction of the noise similar to that
with the filtering method.
Figure 13 shows the result of the inversion.
The residual (Figure 13d) is white, the model
space is well resolved with all the curvatures present (Figure
13a), and the noise model (Figure 13c)
clearly displays the linear coherent noise. The top
and bottom of the residual (Figure 13d) were masked
to avoid edge effects caused by the helical boundary conditions.
Figure 13b shows the reconstructed data.
This result compares favorably with that in Figure
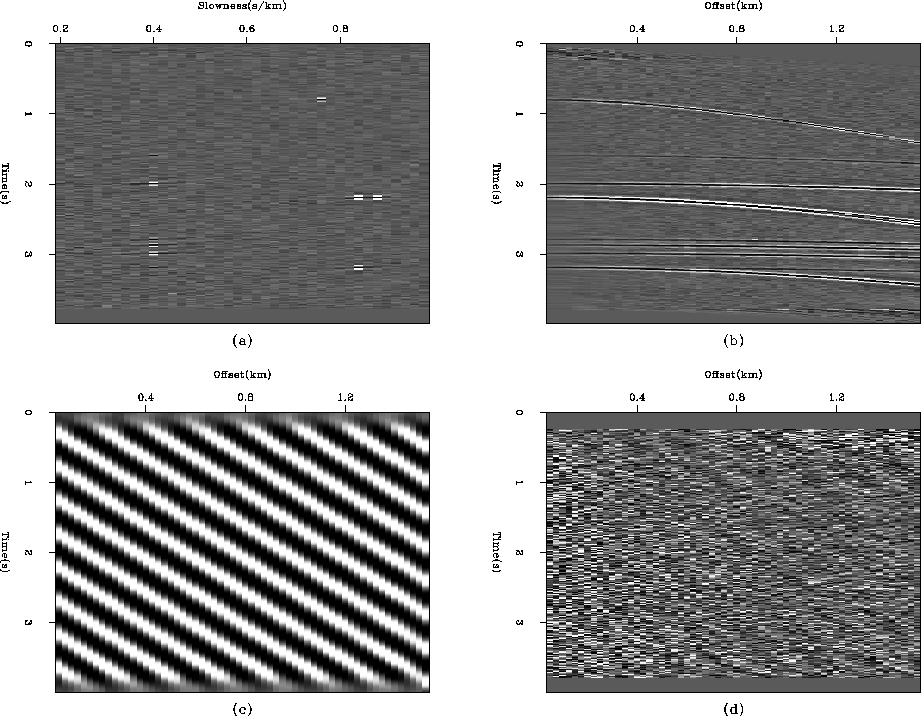
3b. Finally, Figure 14a
compares the amplitude spectrum of the input data (Figure
14a) and of the residual
(Figure 14b). Obviously, the residual energy is
very small.
compsy
Figure 13 Subtracting the coherent
noise in synthetic data. (a) An estimated model space. (b)
The reconstructed data from the model space. (c) The estimated
coherent noise 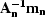 . (d) The residual after inversion.
Click Movie to see how the four panels evolve as the iterations continue.
. (d) The residual after inversion.
Click Movie to see how the four panels evolve as the iterations continue.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)




 compsf
compsf
Figure 14 (a) The amplitude spectrum of
the input data in Figure 1a.
(b) The amplitude spectrum of the residual after inversion.
(c) The normalized objective function. Click Movie to
see how the two panels b and c evolve as the iterations continue.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Subtracting the coherent noise
Up: Subtracting coherent noise
Previous: Subtracting coherent noise
Stanford Exploration Project
4/29/2001
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)