




Next: Subtracting the coherent noise
Up: Guitton: Coherent noise attenuation
Previous: Discussion of the filtering
In contrast to the filtering method which attenuates the coherent noise by
approximating the noise covariance matrix with a PEF,
the following method aims to model the coherent noise
and then subtract it from the input data. This method is
based on the addition of a coherent
noise modeling operator to the fitting goal Nemeth (1996)
as follows:
| 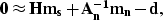 |
(3) |
where H is the signal modeling operator, 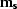 denotes
the model for the signal,
denotes
the model for the signal, 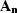 is a PEF that models
the coherent noise present in the data d, and
is a PEF that models
the coherent noise present in the data d, and 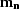 denotes the model for the noise. This method is based on the central assumption that
the data d result from the addition of noise n and
signal s. Thus, ideally, each operator H and
denotes the model for the noise. This method is based on the central assumption that
the data d result from the addition of noise n and
signal s. Thus, ideally, each operator H and 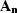 models
a different part of the data. The PEF
models
a different part of the data. The PEF 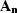 and the operator
H have different physical units. To balance the two operators, I
use the fitting goal
and the operator
H have different physical units. To balance the two operators, I
use the fitting goal
| 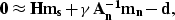 |
(4) |
where
| 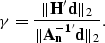 |
(5) |
The constant 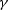 is computed at the first iteration and kept constant.
If I set
is computed at the first iteration and kept constant.
If I set 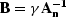 , I can write the fitting
goal in the following form:
, I can write the fitting
goal in the following form:
| 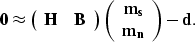 |
(6) |
With 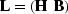 and
and 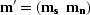 , the fitting goal becomes
, the fitting goal becomes
| 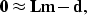 |
(7) |
which leads to the familiar normal equations
| 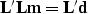 |
(8) |
that can be written as
| 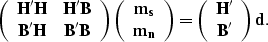 |
(9) |
Based on the results derived in the appendix (equation
(34)), the least-squares inverse of m is
| 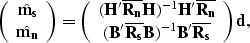 |
(10) |
where 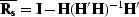 and
and 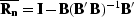 .
.
 is the signal resolution
matrix and
is the signal resolution
matrix and 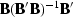 is the noise resolution
matrix. With
is the noise resolution
matrix. With 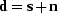 , we have
, we have
| 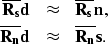 |
(11) |
| (12) |
The operators 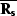 and
and 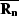 perform signal and noise filtering, respectively.
These operators are also called projectors and discussed in
detail by Guitton et al. (2001) in this report.
We can see that equation (10) for the signal model
perform signal and noise filtering, respectively.
These operators are also called projectors and discussed in
detail by Guitton et al. (2001) in this report.
We can see that equation (10) for the signal model
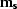 resembles equation (2), except for the
filtering operator
resembles equation (2), except for the
filtering operator 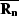 . In other words,
. In other words,
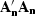 in equation (2) plays the role of
in equation (2) plays the role of
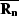 in equation (10). The correct
separation of the signal s and noise n depends on the
invertibility of the Hessians
in equation (10). The correct
separation of the signal s and noise n depends on the
invertibility of the Hessians 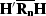 and
and 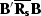 in equation (10) Nemeth (1996).
in equation (10) Nemeth (1996).
The signal/noise separation is perfect if
the signal and noise operators predict distinct parts of the data.
The separation becomes more difficult if the two operators overlap.
However, Nemeth (1996) has proven that the Hessians can
be inverted if we introduce some regularization in the fitting goal.
Hence, the noise prediction can proceed even if signal and noise
are correlated. For instance, if we use a model
space regularization Fomel (1997), we can consider
| 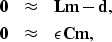 |
(13) |
| (14) |
where
| 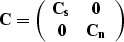 |
(15) |
is the covariance operator for the model m. It is important to
keep in mind that  does not
have to be the same for the noise model covariance and
the signal model covariance. As proven in the
appendix (equation (39)), for
does not
have to be the same for the noise model covariance and
the signal model covariance. As proven in the
appendix (equation (39)), for  constant, the least-squares solution
of the regularized problem is
constant, the least-squares solution
of the regularized problem is
| 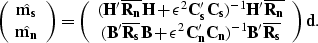 |
(16) |
The regularization operator can also include cross-terms accounting for
the correlation between signal and noise, as follows:
| 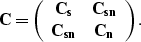 |
(17) |
Although I have not explored this possibility, the regularization
clearly offers the possibility to better separate noise and signal
when the two components are correlated.
With respect to the filtering method, I concluded that a noise model
is not mandatory as long as we can derive it iteratively using a
two-stage process. Accordingly, I used the following
algorithm to accomplish the separation with the subtraction method:
- 1.
- Solve
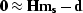 .
.
- 2.
- Estimate a PEF
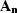 from the residual.
from the residual.
- 3.
- Restart a new inverse problem for the fitting goal in
equation (4).
- 4.
- Stop when the residual has a white spectrum.
With the data in my study, I did not reestimate the PEF iteratively
because I noticed that the first filter was accurate enough to predict the
noise. However, for more complicated noisy events, an
iterative scheme might be preferable. In the next section, I use the
subtraction scheme to separate coherent noise from synthetic and real
data. So far, no regularization is included in the inversion.





Next: Subtracting the coherent noise
Up: Guitton: Coherent noise attenuation
Previous: Discussion of the filtering
Stanford Exploration Project
4/29/2001