Next: Filtering the coherent noise
Up: Approximating the noise covariance
Previous: Approximating the noise covariance
I designed a synthetic case where noise and signal are completely
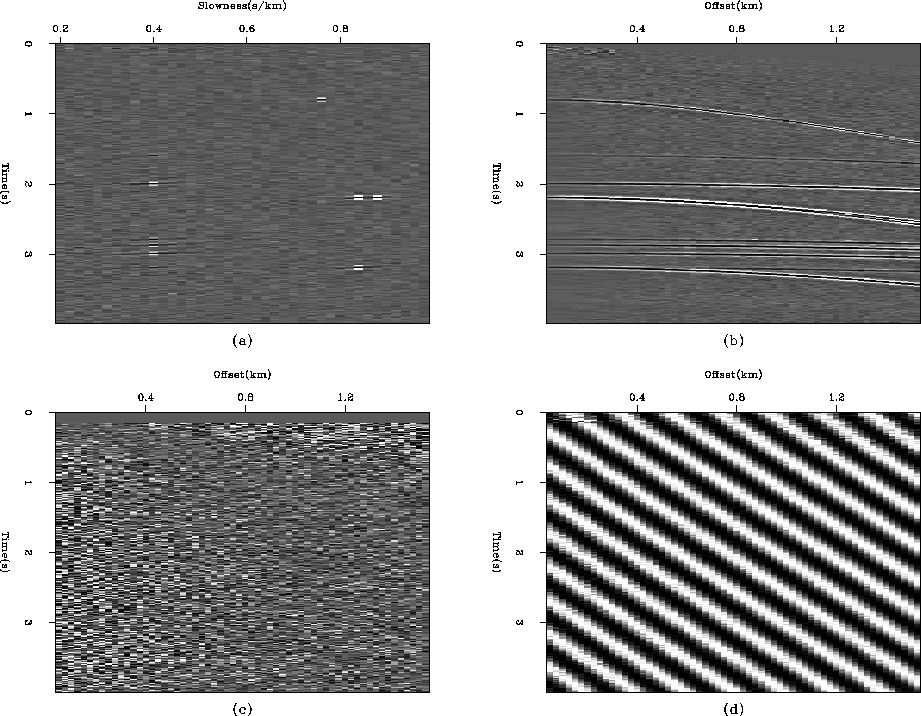
separable. Figure 1a shows the synthetic
CMP gather. The data are made of eleven hyperbolic events overlaid
by a monochromatic event plus some Gaussian zero mean random noise.
H is the velocity stack operator. In the next two sections,
I show that the noise filtering is achieved with or without a noise model.
- Filtering with a noise model
The noise model I use is shown in Figure 2a; it contains
both the monochromatic event and the random noise.
The first parameter I set is the size of the PEF. Because
the coherent noise of this dataset was extremely predictable, it
seemed that a one dimensional PEF with three coefficients PEF should
suffice, but surprisingly, it did not.
Figure 2b displays the inverse spectrum of the
PEF with three coefficients (a=3,1). Clearly, the estimated noise
spectrum does not resemble the coherent noise spectrum in Figure
1b. Using 30 coefficients (a=30,1) significantly
improved the matching (Figure 2c). According to this result,
I chose a 30 coefficients PEF and iterated for the fitting goal
in equation (1).
Figures 3a and b show, respectively, the estimated model
space after inversion and the reconstructed data. No footprint of
the coherent noise appears in either space. In addition, the residual (Figure
3c) is reasonably white, indicating that the
inversion algorithm converged. The ``real'' residual in Figure
3d,
which measures the difference between the input data and the reconstructed
data, displays only the undesirable coherent noise.
datasynth
Figure 1 (a) Synthetic data. (b)
The amplitude spectrum of the data in panel a.




 pefs
pefs
Figure 2 (a) A coherent noise model
used for the synthetic data examples. (b) The inverse
spectrum of the PEF estimated from the noise model, with 3
coefficients. (c) The inverse spectrum of the PEF estimated from
the noise model, with 30 coefficients.




 c-synth
c-synth
Figure 3 Filtering the coherent
noise in synthetic data with a noise model. (a) An estimated model
space. (b) Reconstructed data using the model space. (c) The weighted residual
(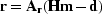 ) after inversion. (d) The difference between
the input data in Figure 1a and the reconstructed
data in 3b.
) after inversion. (d) The difference between
the input data in Figure 1a and the reconstructed
data in 3b.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





- Filtering without a noise model
The PEF (a=30,1) is now iteratively updated. The first stage
of this method is to iterate with no PEF in the fitting goal and
then to estimate the PEF after a certain number of iterations from the
residual. I iterated 10 times before estimating the filter. Figure
4a displays the residual after 10 iterations
and its corresponding spectrum in Figure 4b.
As expected, the residual is mostly noise, which makes the
first PEF estimation reliable.
In the second stage, after the first PEF calculation, the model space
is reset to zero and the conjugate gradient (the iterative solver I
used) is restarted. Figure 4c shows the
residual after the first iteration. The coherent noise has been
properly attenuated. The spectrum in Figure 4d
shows almost no trace of the monochromatic event. I then recomputed
the PEF after every 10 iterations. The outcome of this
process, displayed in Figure 5, is comparable to
that in Figure 3.
s-synth-rec
Figure 4 (a) The residual of the
filtering scheme without a PEF after 10 iterations. (b) The amplitude
spectrum of the residual. (c) The residual after the first iteration
with a PEF (estimated from the residual in 4a) in
the fitting goal. (d) The amplitude spectrum of the residual in
4c. The noise spectrum has vanished from the residual.




 c-synth-rec
c-synth-rec
Figure 5 Filtering the coherent
noise in synthetic data without a noise model.(a) An estimated model
space. (b) Reconstructed data using the model in
5a. (c) The weighted residual
(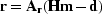 ) after inversion. (d) The difference between
the input data in Figure 1a and the reconstructed
data in 5b.
) after inversion. (d) The difference between
the input data in Figure 1a and the reconstructed
data in 5b.










Next: Filtering the coherent noise
Up: Approximating the noise covariance
Previous: Approximating the noise covariance
Stanford Exploration Project
4/29/2001



![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)