




Next: Spline regularization
Up: Iterative data regularization
Previous: SeaBeam water bottom
As demonstrated in Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , B-splines provide an
exceptionally accurate method of forward interpolation. In this
section, I discuss how this choice of the forward operator affects the
regularization part of the problem. In the case of B-spline
interpolation, the forward operator
, B-splines provide an
exceptionally accurate method of forward interpolation. In this
section, I discuss how this choice of the forward operator affects the
regularization part of the problem. In the case of B-spline
interpolation, the forward operator 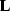 is a cascade of two
operators: recursive deconvolution
is a cascade of two
operators: recursive deconvolution 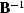 , which converts the
model vector
, which converts the
model vector  to the vector of spline coefficients
to the vector of spline coefficients
 , and a spline basis construction operator
, and a spline basis construction operator 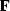 .System (
.System (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to
) transforms to
| 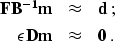 |
(10) |
| (11) |
We can rewrite (10-11) in the form that
involves only spline coefficients:
| 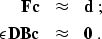 |
(12) |
| (13) |
After we find a solution of system (12-13),
the model  will be reconstructed by the simple convolution
will be reconstructed by the simple convolution
| 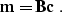 |
(14) |
This approach is clearly just another version of model preconditioning.
The inconvenient part of system (12-13) is the
complex regularization operator 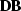 . Is it possible to avoid
the cascade of
. Is it possible to avoid
the cascade of 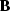 and
and 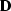 and to construct a
regularization operator directly applicable to the spline coefficients
and to construct a
regularization operator directly applicable to the spline coefficients
 ? The answer is positive. In the following subsection, I
develop a method for constructing spline regularization operators from
differential equations.
? The answer is positive. In the following subsection, I
develop a method for constructing spline regularization operators from
differential equations.





Next: Spline regularization
Up: Iterative data regularization
Previous: SeaBeam water bottom
Stanford Exploration Project
12/30/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , B-splines provide an
exceptionally accurate method of forward interpolation. In this
section, I discuss how this choice of the forward operator affects the
regularization part of the problem. In the case of B-spline
interpolation, the forward operator
, B-splines provide an
exceptionally accurate method of forward interpolation. In this
section, I discuss how this choice of the forward operator affects the
regularization part of the problem. In the case of B-spline
interpolation, the forward operator ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) transforms to
) transforms to